-
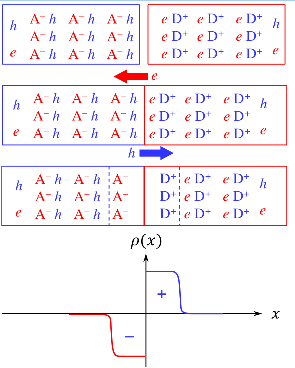
p-type 전자 : diffusion-drift에 의해 n-type로 이동
-
n-type 전자 : potential이 낮아져 더 많은 양의 캐리어가 p-type으로 diffusion 가능
-
JN=JN∣drift(p⇒n)+JN∣diff(n→p)=JN∣diff (potential을 넘어간 diffusion 분량만 전류로 작용)
-
JP=JP∣diff (potential을 넘어간 diffusion 분량만 전류로 작용)
-
built-in potential이 q(VBI−VA)로 감소, 이동하는 캐리어 수가 증가 = 전류 흐름
-
원래 페르미 준위보다 p는 내려가고, n은 올라감 : −qVA만큼 차이나게 됨 (p방향에 +전압을 걸어주어 ptype 준위가 내려갔으므로 전위차는 -가 됨)
-
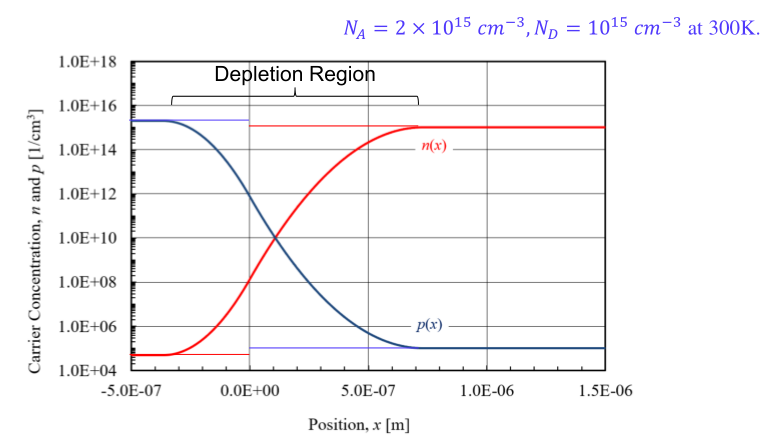
minority carrier injection : forward bias에 의해 potential barrier가 낮아지면서 majority carrier가 minority carrier 자리로 이동하게 된다.
-
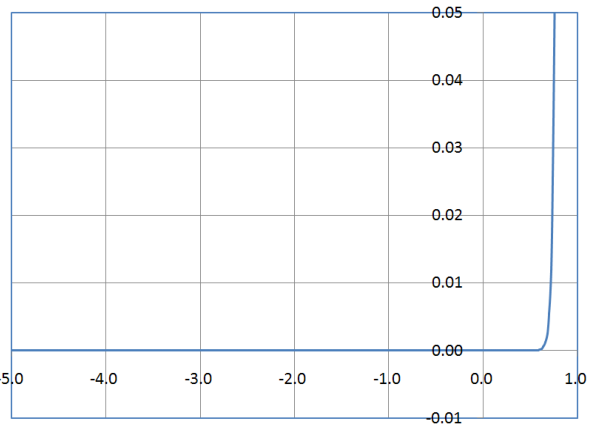
eVA/VT에 비례한 전류 형성 : carrier injection에 의해 junction 근처에서 exponential한 캐리어 분포 형성