728x90
4. Analysis of Feedback
1. Basic Equations of Control
- open loop system : disturbance(외란)에 민감하고, steady state error가 점점 증가(누적)

- 출력
- Transfer function (외란은 무관)
- 오차
- closed loop system : 피드백을 이용하여 외란 제거, 안정도 높음

- 외란 W와 센서 노이즈 V가 같이 존재
- Controller 입력
- 피드백
- 출력
- 오차
- 전달함수
- Open loop / Closed loop의 안정도
-
Open loop system의 전달함수
- Plant G(s)의 pole이 우반면에 존재(불안정)시 전체 시스템 T(s) 역시 불안정하게 됨
- ex. 이면 둘을 곱해도 unstable pole을 갖게 됨
- D의 를 G(s)의 pole과 동일하게하여 식에서는 지울 수 있다 해도,
오차에 의해 실제 시스템에서는 둘을 정확하게 일치하는 것이 불가능하다.
그러므로 open-loop system의 불안정 pole을 지우는 것은 사실상 불가능함.
-
Closed loop system의 전달함수
- 라 가정
- 전달함수의 pole 식은 으로 정리된다.
- 즉 G(s)의 b(s)가 unstable pole을 갖더라도 의 적절한 조정으로 전달함수의 2차 방정식은 stable하게 조절 가능
-
- Disturbance Rejection : 외란 W에 의한 오차
-
Open-loop system disturbance
- 시스템 G와 외란 W 모두 조절이 불가능한 요인이므로, steady state에서의 오차는 조절 불가
-
Closed-loop system disturbance
- 제어 가능한 을 가능한 크게 만들면 Open loop 대비 오차를 줄일 수 있음
- steady state Error
-
- Sensitivity
-
임의 시스템을 장시간 구동하면 시스템에 변형이 발생
-
sensitivity : 만약 Plant G에 변형이 왔을 경우 전체 시스템(전달 함수)에 발생하는 변형
- 일 때 의 정도
- sensitivity T to G :
-
Open-loop system의 경우
- (Controller 변화는 없다고 가정)
- 이므로
- 즉 Open-loop system의 stability = 1 : Plant의 변화가 그대로 system에 반영
- (Controller 변화는 없다고 가정)
-
Closed-loop system의 경우
- Controller 의 조정에 따라 sensitivity의 감소 가능
-
2. Control of Steady State Error to Polynomial Input
- Stable Unit negative Feedback system

- steady-state error :
(Final Value Thm.)
- 입력 신호에 따른 steady-state error의 응답

- (a) unit step input :
- 일정한 값 입력 > 일정 위치 목표
- Position error Constant :

- (b) unit ramp input :
- 일정 기울기 입력 > 일정 속도 목표
- velocity error Constant :

- (c) unit parabola input :
- 2차 미분이 일정 > 일정 가속도 목표
- Acceleration error Constant :
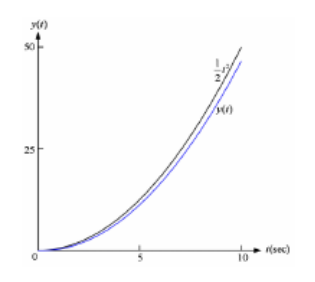
- (a) unit step input :
- System Type
- pole값이 0이 되는 식의 차수
- 라고 할 때, 이 시스템을 n차 시스템이라고 정의
- 0차 시스템 :
- 1차 시스템 :
- n차 시스템
- 입력 일 때
- n > k :
- n < k :
- n = k = 0 :
- 시스템 차수보다 낮은 차수의 오차상수는 0, 높은 차수의 오차상수는 무한대가 된다.
3. PID control

- Closed-Loop system의 컨트롤러의 전달함수를 D를 조절하여 오류값을 비례(proportional) - 적분(Integral) - 미분(Derivative)하는 컨트롤러
- controller
- P controller : 오류값에 비례하는 제어
- (type 0)
- position error const.
- steady-state error
- PI controller : 오류값에 비례+미분 제어
- (type 1)
- position error const.
- unit step에 대한
- I controller에 의해 위치의 steady-state error 제거
- velocity error const.
- unit ramp에 대한
728x90