Disk Structure

• Magnetic Disk : HDD 등
  • Transfer Rate : 저장 장치 - 커뮤퍼 사이의 데이터 전송 속도
  • Positioning Time(random-access time) : 디스크 암이 목표 실린더에 도달하는 시간(seek time)과 목표 섹터에 도달하는 시간(rotational latency)
  • head crush : 디스크 암과 디스크가 맞닿는 현상
• Access Latency = Average access time = 평균 탐색 시간 + 평균 지연
• Average I/O time = average access time + (transfer amount / transfer rate) + controller overhead

• Logical block
  • 디스크는 1차원의 logical block의 배열로 관리
  • 논리적 주소가 물리적 주소를 의미하지는 않음
  • garbage collector : 쓰레기 값이 저장된 block을 초기홫

Disk Scheduling

• seek time의 최소화
• request queue에 실린더 위치가 순서대로 입장
  • ex) 98, 183, 37, 122, 14, 124, 65, 67
  • head 위치는 53이라고 가정
• FCFS : 큐에 들어오는 순서대로 접근
• SSTF : 현 위치에서 seek time이 가장 짧은 위치로 먼저 접근
  • SJF와 유사 : starvation 문제가 생길 수 있음
• SCAN : 디스크 암이 logical array의 양 끝 번갈아 왕복하며 처리
  • elevator algorithm이라고도 부름
  • 디스크 암과 실린더 위치에 따라 장시간 대기해야 하는 경우가 생길 수 있음
• C-SCAN
  • 실린더의 처음부터 끝까지 순서대로 처리
  • 실린더 끝까지 탐색하면 다시 처음으로 이동한 뒤 끝까지 이동하면서 처리
  • 실린더 양 끝을 왕복하는 SCAN의 단점이 어느정도 해결
• C-LOOK
  • Look : 큐의 최대/최소점에 도달하면 실린더는 반대 방향으로 탐색
  • C-Look : Look으로 동작하되, C-SCAN과 같이 큐 최대점 도달 시 다시 최소점으로 이동한 후 처리

Disk Management

• Low-Level Formatting
  • 물리적 포맷이라고도 함
  • 디스크를 R/W 동작이 가능한 섹터로 분할
  • 각 섹터는 정보, 데이터, ECC(Error Correction Code)가 저장
• 파티션 : 디스크를 논리적 단위로 분할
  • 논리적 포맷 혹은 "파일 시스템을 만든다" 라고도 함
  • 효율성을 위해 파일은 클러스터 단위로 처리 (디스크 > 블록, 파일 > 클러스터)
• 부팅 과정
  • 롬에 저장된 BootStrap이 부팅 시 호출됨
  • 디스크 0번 섹터(MBR)의 프로그램이 부트스트랩을 호출하는 기능을 함(Bootstrap Loader)

• Swap Space management
  • page 파일을 만들어 관리하거나, swap 파티션을 할당하여 관리
  • swap map : 커널은 swpap 사용 방식을 추적
  • swap 공간이 없다 = 메모리 가용량이 없음 >> process kill or crash

RAID

• 저가의 디스크를 다수 연결하여 고성능 구현 (scale - out)
  • mean time to failure : 고장 확률이 높아짐
  • mean time to repair : 추가적인 고장 확률이 높음
• 다수의 디스크를 병렬로 기록 시 : 읽는 속도가 증가
• ex. 디스크의 mean time to failure = 100000, mean time to repair = 10
  • mean time to data loss = 100000^2 / ( 2 * 10 ) = 500 * 10 ^ 6 (약 57000년)
  • 실제로는 저장장치가 완전히 독립적이지 않으므로 이보다는 짧아짐

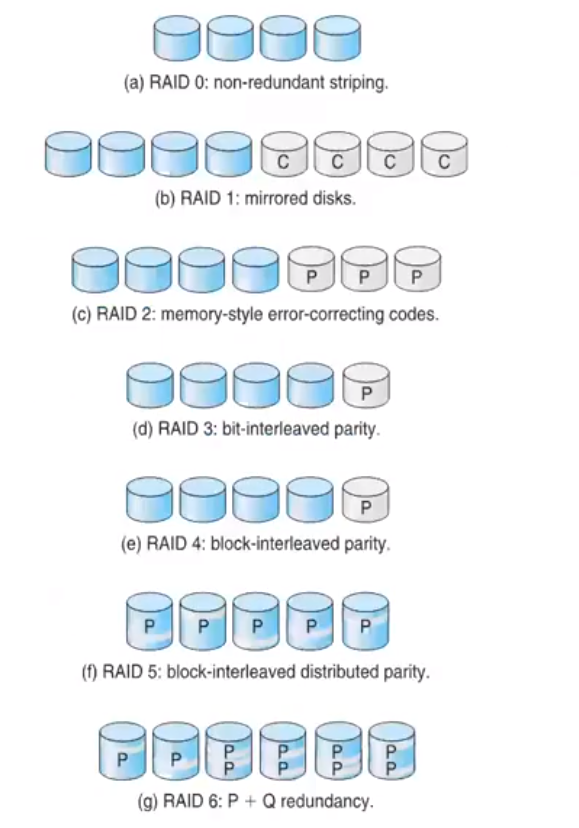
• Disk striping : 여러 개의 저장 장치를 하나의 단위로 취급
• RAID를 통해 성능을 높이거나, 저장장치의 신뢰성을 높일 수 있음
• RAID 0
  • 큰 데이터를 각 저장장치로 분산
  • 디스크 중 하나가 고장나면 전체 데이터가 손실
• RAID 1
  • Mirroring 혹은 Shadowing으로 호칭
  • 각 디스크의 복사본을 저장
  • 한 쪽이 고장나도 안전한 대체 가능
• RAID 2 : ECC code를 사용
• RAID 3 : Bit Interleaved Pairty
• RAID 4 : Block Interleaved Parity / Parity disk가 고장 시 전체 데이터 손실
• RAID 5 : RAID 4에서 parity를 각 디스크로 분산
• RAID 6 : Parity 정보를 이중으로 기록
• RAID 1 + 0 / RAID 0 + 1
  

  

  • 전자는 Striped Mirror, 후자는 Mirrored stripe
  • 신뢰성과 성능 모두를 추구
  • 디스크 구조상 RAID 1 + 0이 더 안전
• hot-spare : 비상용 디스크 / RAID 중 디스크 고장 시 빠른 대체

Stable Storage Implementation

• 데이터를 저장할 때 안전하게 보관하는 상태
• 1개 이상의 비휘발성 저장소에 복원 가능하도록 데이터를 저장
• Disk Write의 결과
  • 정상 작동
  • 부분 실패
  • 완전 실패

Virtual address

• virtual address space : 프로세스 내의 주소 표현을 논리적으로 나타냄
  • 0으로 시작하여 연속적으로 표현
• demand paging
  

  

  • 프로세스의 필요한 페이지만 필요할 때 할당하는 것
  • I/O가 덜 필요하거나 아예 쓸 필요가 없음
• page fault
  • logical memory에서 page table 접근 시 invalid한 경우
  • 다른 page table을 참조하게 되는 경우

• demand paging 단계
  • 레지스터와 프로세스 상태 저장
  • page fault로 인한 인터럽트 여부 확인
  • page table의 valid 여부, page 위치 확인
  • 저장소에서 frame으로 read 요청
    • 요청을 큐에 할당
    • 장치의 seek/latency time동안 대기
    • page를 free frame으로 전송
  • 대기 중일 때는 CPU는 다른 사용자에게 할당
• demand paging 시의 EAT
  • 주된 동작 : 인터럽트 서비스, page read, process restart
  • page fault rate p를 가정 (p=0 : no page fault)
  • EAT = (1 - p) * 메모리 접근 + p * (page fault overhead + swap In + swap Out)

Copy on Write

• 프로세스 fork 시 부모 - 자식 프로세스가 같은 page를 공유하게 하는 것
  • 자식 프로세스 생성 시에는 프로세스 공간을 복사하지 않음
  • 한 쪽의 프로세스가 write 동작 시 page 복사가 일어남
• page replace
  • page의 과한 할당을 방지
  • page overhead를 줄이기 위한 modify(dirty) bit 사용 - 수정된 page만 write

Page replace

• 제한된 메모리 상의 process 할당 시 page 전환이 필요
• 여유 공간이 없을 경우 page를 전환하여야 함
• page replace 단계
  • page 할당이 필요할 때, free frame을 탐색
  • free frame이 없을 경우, 제거될 frame(victim frame)을 선택
  • victim frame은 저장소로 swap out / 필요 데이터는 그 자리로 swap in
• replace algorithm
  • frame - allocation : 프로세스당 프레임을 얼마나 할당할지, 어떤 프레임을 재할당할지
  • page - replacement : page fault rate를 최소한으로 하도록
  • reference string : 접근한 page 기록을 저장하여 replace 알고리즘에 사용
• FIFO
  

  

  • 가장 먼저 들어온 page를 replace
  • page fault는 10번 발생 (처음부터 계속 page가 없어 replace함)
  • belady's anomaly : frame 수가 늘어나면 오히려 page fault가 많아질 수 있음
• Optimal algorithm
  

  

  • 가장 오래 사용될 페이지는 유지
• Least Recently Used(LRU)
  

  

  • 가장 사용되지 않은 데이터를 교체
  • 미래를 예측하는 Optimal과 달리 과거 데이터를 활용
• second chance algorithm
  

  

  • FIFO와 유사
  • reference bit가 0이면 교체
  • reference bit가 1이면 0으로 변경
  • enhanced second chance
    • (reference, modify)로 2개 bit 할당
    • (0, 0) : replace
    • (0, 1) : replace 전에 메모리 write
    • (1, 0), (1, 1) : 다음 접근 시 replace
    • ex. (1, 1) > (0, 1) > (0, 0) - 3번의 반복을 통해 victim frame이 됨

Buddy System

• $2^n$ allocater를 이용한 메모리 할당
• Slab : 1개 이상의 연속된 page
  • 캐시는 하나 이상의 Slab로 구성
• prepaging
  • page fault 방지를 위해 미리 page 할당
• program 구조
  • 2차원 array int[a, b]를 가정
  • 각 row에는 page가 저장됨
  • 위 코드는 col마다 접근하기 때문에 a * b번의 page fault가 발생하나, 아래 코드는 page fault가 row 개수만큼만 발생

for(j=0;j<a;j++)
    for(i=;i<b;i++)
        data[i, j]=0


for(i=;i<b;i++)
    for(j=0;j<a;j++)
        data[i, j]=0

• I/O Interlock
  • 프로세스가 I/O 장치를 접근할 때, 해당 프로세스가 swap되는 경우
  • 프로세스는 물리적 주소가 할당되기 전이지만, 데이터는 여전히 입력되어야 하는 상태가 됨
  • 이로 인한 문제를 방지하기 위해 프로세스의 해당 page를 swap되지 못하도록 함 (Pinning)

• 실행된 프로그램은 메모리에 적재됨
  • 메모리에 적재되는 데이터 : 명령어, parameter, parameter가 저장된 주소
• 메모리가 처리하는 data stream
  • read : address
  • write : address + data
• 보통 레지스터 접근은 1 clock 내에 처리
  • 메모리 접근은 레지스터 대비 긴 시간이 걸리기 때문에, 중간에 캐시 메모리를 이용하여 병목 현상을 보완
• 메모리 보호
  

  

  • 프로세스가 접근 가능한 주소에 제한
  • ex. 프로세스 할당 시 주소(base) 레지스터와 함께 할당 공간의 제한(limit) 레지스터를 같이 할당
  • base 아래 혹은 base + limit 위의 주소 접근 시 인터럽트를 호출하여 process 삭제

Address Binding

• 프로그램 생성마다의 address binding 단계
  • 소스 코드 : 변수 주소를 symbolic하게 표현
  • 컴파일된 코드는 주소를 relocatable address로 bind
    • relocatable addreess : 프로그램 시작 지점에서의 상대적 offset 주소
  • 링커 / 로더 : 메모리에 적재된 프로그램에 실제 주소 할당
• 주소가 결정되는 단계
  • compile time : 만약 이 단계에서 static한 주소 명시가 된 경우 compile 단계에서 주소 할당
  • Load time : compile time에서 할당되지 않은 주소를 relocatable address로 할당
  • Execution time : 실행 중 새롭게 할당되는 주소 관리

MMU(Memory-Management Unit)

• Logical Address : 프로세스가 바라보는 주소, 가상 주소라고도 함
• Physical Address : 메모리상의 실제 주소
• CPU에서 명령 수행 시 logical address에 접근
• MMU에서 logical address-physical address를 변환
• simple scheme
  • MMU에는 relocation register에 값이 할당
  • CPU에서 logical address 접근 시, relocation register 값만큼 offset을 주어 physical address에 접근하게 함
  • ex. relocation register에 10000이 저장, CPU에서 ld 365 명령 실행 시 실제로는 10365 주소의 메모리에 접근
  • dynamic relocation : 만약 해당 주소에 접근 불가할 경우 relocation register 값을 변경

• static linking
  • binary 코드 생성 시 라이브러리를 모두 포함
  • 프로그램이 무거워지고, 라이브러리가 중복 사용되는 경우 메모리 비효율성
• Dynamic Linking
  • 중복 사용되는 라이브러리는 메모리에 미리 적재
  • 해당 라이브러리를 사용하는 프로세스는 필요할 때마다 별도로 호출
  • stub : Dynmic link를 찾는 루틴

Variable Partition

• hole : 가능한 메모리 블럭
• 프로세스를 단순히 연속 할당 시 메모리 관리가 비효율적이 될 수 있음
• Dynamic Storage Allocation
  • First fit : 할당 가능한 첫번째 hole에 프로세스 할당
  • Best fit : 할당 가능한 최적의 hole에 프로세스 할당
  • Worst fit : 가장 큰 hole에 프로세스 할당
• Fragmentation : 할당으로 인해 생기는 메모리 비효율
  • external fragmentation : 전체 메모리 여유 공간은 충분하나, 연속적이지 않아 할당이 불가능한 경우
  • internal fragmentation : 요청받은 프로세스 크기보다 할당 공간이 약간 큰 경우, 메모리 차이만큼의 공간은 너무 작아서 활용이 불가능
  • 50% rule : 메모리를 N개 block으로 할당한다고 할 때, 절반 가량은 fragmentation에 의해 사용 불가
• Compactation : external fragmentation의 제거
  • 모든 hole을 하나의 공간으로 합침
  • relocation이 동적일 때, excution time에 동작함

Segmentation

• 메모리를 segment라는 논리적 단위로 할당
• segmentation 구조 : <segment-number, offset>
  • segment table : 각 segment의 base, limit 주소를 저장, segment number로 접근
    • base : segment의 시작 주소
    • limit : segment의 길이, 이 주소를 초과하여 접근시 error

• segment number(s)는 segment table로 접근
• offset은 segmnet table의 limit과 비교
  • limit 초과 시 addressing error
• segment table의 base와 offset이 합쳐져 실제 메모리로 접근하게 됨

Paging

• 메모리의 주소를 고정 크기로 나누어 할당하는 것
  • 연속적 할당이 아니므로 fragmentation 문제가 없음
• frame : 물리적 메모리에 접근하는 block 단위
• page : 가상의 메모리에 접근하는 block 단위
  • page 요청 > frame 요청 > OS는 빈 frame를 찾아 할당
• addresss translation
  • CPU에 의해 생성되는 주소는 page number / offset으로 구분
  • page number : page table에 접근하기 위한 index >> frame number를 탐색하여 page offset과 조합
  • page offset : 실제 메모리 주소에 접근하기 위해 사용
  • page size를 4kb(2^12)라 가정
  • 32bit system에서 page offset d = 12가 되고, page number p = 20이 됨
• CPU가 logical 접근
  • page table에 p index 값을 접근, 해당 값을 frame에 전달
  • offset d만큼의 주소를 더해 접근
  • frame offset d만큼의 주소를 더해 메모리 접근

• internal fragmentation = page size - page 할당 후 남는 크기만큼
• worst fragmentation = 1 frame - 1 byte
• average fragmentation = frame size * 0.5
• Page table
  • page table base register(PTBR) : page table 위치를 가리킴
  • page table length register(PTLR) : page table의 크기를 나타냄
• TLB(Transition look-aside buffer)
  • CPU에서 메모리 접근 시 page table을 거치기 때문에 속도 문제가 발생
  • associative memory라고도 하며, 논리 - 물리 메모리 주소의 변환 결과를 미리 저장
  • TLB에 데이터 존재시(hit) 메모리 접근, 없을 경우 page table 접근
• Effective Access TIme(EAT)
  • hit ratio : TLB에서 데이터를 찾아올 수 있는 비율 (ex. hit ratio 80% : 100번 탐색 중 80번은 TLB로 접근)
  • EAT = hit ratio * TLB access time + (1 - hit ratio) * memory access time
• memory protection
  • page table에 read/write bit를 설정하여 프로세스 접근 시 읽기/쓰기 가능 여부를 설정
  • valid-invalid : 페이지가 프로세스의 주소 공간에 할당되었는지 여부를 확인

Page Table Structure

• hirearchial page table
  

  

  • page table 탐색의 overhead 감소
  • page table의 page table을 구성
  • logical address는 inner page + outer page + offset과 같이 구성
• hased page table
  

  

  • page table을 hash table로 구성
• inverted page table
  • 논리 주소가 아닌 물리적 주소로 page table 구성
  • virtual address를 이용하여 shared page 구현

Swapping

• 사용되지 않는 프로세스를 보조 저장장치에 저장하여 메모리를 관리
• context switching time = 전송 시각 * process 크기 * 2

Jacobi Iterative Method

• 행렬 Ax=b를 풀 때
  • 초기 가정 $x^0$을 가정하고, $x^k$에 대해 k의 극한 계산
• Jacobi Iterative method
  • $x_i=\sum_{j=1,j\not ={i}}(-\frac{a_{ij}x_j}{a_{ii}})+\frac{b_i}{a_{ii}}$
  • 2x2 행렬에 대해, $\\a_{11}x_1+a_{12}x_2=b_1\\a_{21}x_1+a_{22}x_2=b_2$
  • 위 식에서 $\\x_1=\frac{b_1}{a_{11}}-\frac{a_{12}}{a_{11}}x_2\\x_2=\frac{b_2}{a_{22}}-\frac{a_{21}}{a_{22}}x_1$
  • $x_1^{n+1}=\frac{b_1}{a_{11}}-\frac{a_{12}}{a_{11}}x_2^n\\x_2^{n+1}=\frac{b_2}{a_{22}}-\frac{a_{21}}{a_{22}}x_1^n$
  • 계산된 해에 대해 $\frac{||x^k-x^{k-1}||_\infty}{||x^k||_\infty}$가 일정 오차 이하가 될 때까지 반복
• More general representation
  • 행렬 A를 $A=D-L-U$로 분리
    • D : 대각행렬 / L : Lower Triangle / U : Upper Triangle
  • $Ax=b$를 계산하면 $x=D^{-1}(L+U)x+D^{-1}b$, 즉 $x=Tx+c$꼴로 변환
  • $\rho(T)<1$ 혹은 $||T||_\infty$임을 증명하면 $x^k=Tx^{k-1}+c$가 수렴함을 증명할 수 있다.

Gauss-Seidel Method

• $x_1^{n+1}=\frac{b_1}{a_{11}}-\frac{a_{12}}{a_{11}}x_2^n\\x_2^{n+1}=\frac{b_2}{a_{22}}-\frac{a_{21}}{a_{22}}x_1^{n+1}$

• $x^n=x$로 수렴하기 위한 조건

  • $T^nx^0$가 0으로 수렴
  • $S^nc$는 x로 수렴
  • 즉 $\rho(T)<1,\ ||T||_2<1,\ ||T||_\infty<1$중 하나를 만족
    • 앞으로 갈수록 sharp한 수렴, 계산은 복잡
  • 한 열에서 사용한 결과값을 바로 다음 열에 사용하므로 계산 시간이 줄어듬
  • $\begin{bmatrix} b1\\ b2 \end{bmatrix}=\begin{bmatrix} a_{11}\ 0\\ a_{21}\ a_{22} \end{bmatrix}+\begin{bmatrix} 0\ a_{12}\\ 0\ 0 \end{bmatrix}$

• $Dx^{n+1}=Lx^{n+1}+Ux^n+b$

  • D : A행렬의 대각선 원소 / L : L행렬 대각원소의 아랫부분 / U : L행렬 대각행렬의 윗부분

• $\rho(T)<1$일 때, $(I-T)^{-1}$을 만족

  • $S_n=(I-T)^{-1}=I+T+T^n+...+T^n$
  • $(I-T)S_n=I-T^{n+1}$
  • n이 발산하면 S는 I로 수렴

• fixed-point iteration 형태의 표현
  • $x^k=Tx^{k-1}+c$
  • jacobi iteration : $T_j=D^{-1}(L+U)$
  • gauss-seidel : $T_g=(D-L)^{-1}U$

Successive Over Relatxation(SOR)

• $x^{n+1}=(1-w)x^n+wx_g^{n+1}$
  • w : relaxation parameger
  • $w_g$ : gauss-seidel로 계산한 값
• Residual Vector
  • gauss-seidel method에서 $x^{n+1}=\frac{1}{a_{11}}[-a_{12}x_2^n+b_1]$
  • 즉 $a_{11}x_1=a_{11}x_1^{n+1}-a_{11}x_1^n\\=-a_{11}x_1^n-a_{12}x_2^n+b_1=r_1^n$으로 정의
  • residual form : $x^{n+1}=x^n+D^{-1}r^n$
  • SOR residual form : $x^{n+1}=x^n+wD^{-1}r^n\\x^{n+1}=(1-w)x^n+wD^{-1}(Lx^{n+1}+Ux^n)$

support vector machine

• 임의 dataset의 decision boundary 설정 시, boundary와 가장 가까운 data point와의 간격(margin)을 최대로 하는 선을 정의
• $\theta^T\vec{x}=w^T\vec{x}+b$
  • $\theta_0=b$로 해석
  • $w^T\vec{x}=\theta_1x_1+...+\theta_nx_n$
  • y = -1 or 1로 나타남(binary classification)
• 벡터 $\vec{p}=x_n-x$에 대해
  • $\frac{\vec{w}^T}{||w||}\vec{p}=\frac{1}{||w||}[\vec{w}^Tx_n+b-(wx^T+b)]=\frac{1}{||w||}$
  • $|\vec{w}^Tx_n+b|=1$인 조건 하에 $\frac{1}{||w||}$를 최대화
    • $|\vec{w}^Tx_n+b|=y_n(\vec{w}^Tx_n+b)$, $\vec{w}^Tx_n+b$의 부호에 의해 +1 혹은 -1로 값이 결정됨
    • 벡터 $\vec{w}$에 대해 $||\vec{w}||^2=w^Tw$
    • $\frac{1}{||w||}$의 최대화 = $||w||$의 최소화, 즉 미분값을 최소화하게 되므로 $||w||=\frac{1}{2}w^Tw$

Lagrange multiplier

• $f(x, y) = ax + by = k$, $g(x, y) = x^2+y^2 = r^2$인 함수 f, g를 가정
  • f와 g가 접하게 되면 gradient가 동일 : $\nabla f = \lambda\nabla g$
  • $\lambda$ : lagrange multiplier
  • $L(x,y,\lambda) = f(x,y) - \lambda(g(x,y) + c)$
• $\nabla L=\frac{\partial L}{\partial x} = \frac{\partial f}{\partial x} - \lambda\frac{\partial g}{\partial x} = 0$
  • $\frac{\partial f}{\partial x}=\lambda\frac{\partial g}{\partial x}$
• SVM 계산에 있어 $f=\frac{1}{2}w^Tw$, $g=y_n(x^Tx_n+b)-1\geq0$
  • $L(w,b,\lambda) = \frac{1}{2}w^Tw+\sum\lambda_i[-y_i(w^Tx_i+b)-1]$
  • $\frac{\nabla L}{\partial w}=0=w-\sum\lambda_iy_ix_i\\\rArr w=\sum\lambda_iy_ix_i$로 SVM weight w 계산
  • $\frac{\nabla L}{\partial b}=0=\sum\lambda_iy_i$
• $L(w,b,\lambda) = \frac{1}{2}w^Tw+\sum\lambda_i[-y_i(w^Tx_i+b)-1]$에서
  • $w=\sum\lambda_iy_ix_i$
  • $\sum\lambda_iy_i=0$
  • $L(w,b,\lambda)=\sum\lambda_i+\frac{1}{2}w^Tw-\sum\lambda_iy_iw^Tx_i\\=\sum\lambda_i-\frac{1}{2}w^Tw$

How to solve SVM

• SVM : $y(w^Tx_i+b)\geq1$일 때 $\frac{1}{2}w^Tw$의 최소값을 계산하는 것
• Lagre multiplier : $L(w, b, \lambda) = \frac{1}{2}w^Tw-\sum\lambda[y_i(w_i^Tx_i+b)-1]$
  • $sup_\lambda L(x, \lambda)$ : $\lambda$에 대해 가질 수 있는 L의 최댓값을 찾는 것
• SVM의 해 $p^*=inf_\lambda sup_\lambda L(x, \lambda)$ : L이 가질 수 있는 최댓값 중 하한선
  • $sup_\lambda L(x, \lambda)$는 $\sum$식이 음수일 땐 $\frac{1}{2}w^Tw$지만, 양수일 땐 무한으로 발산
  • sup값이 가질 수 있는 하한선은 즉 $\frac{1}{2}w^Tw$이 됨
• Lagrange dual function : $g(\lambda)=inf_{w,b}L(w,b,\lambda)$인 함수 g를 정의
  • $\lambda \geq0$일 때 $g(\lambda)\leq p^*$ : $g=inf\ L\leq L(x, \lambda)$이기 때문
  • $p^*$를 구하기 어렵다면 $g(\lambda)$를 구한 후 $p^*=sup_\lambda g(\lambda)$를 계산하는 방법도 있음
• $g(\lambda)=inf_{w,b}L(w,b,\lambda)$
  • $\frac{\partial L}{\partial w}=w-\sum\lambda_i y_ix_i=0$
  • $\frac{\partial L}{\partial b}=\sum\lambda_iy_i=0$
  • 즉 $g(\lambda)=-\frac{1}{2}w^Tw+\sum\lambda_i$

Memory hierarchy

• 주 메모리에는 프로그램과 데이터가 저장
• 한편 모든 프로그램을 할당하기에는 메모리 용량이 모자람
• 주 메모리는 CPU와 연결
  • 현 시점에서 사용되는 프로그램/데이터가 주 메모리에 저장
• 보조 저장소에는 그 외의 데이터가 저장
• 싸고 빠를수록 CPU에 가깝고(레지스터, 메모리, ...), 느리고 쌀수록 주변장치에 저장(HDD, SSD, ...)

Main memory

• CPU가 동작시키는 프로그램과 데이터가 저장
• Static RAM / Dynamic RAM
  • 비용, 전력, 접근 시간 등에서 차이
• ROM : 초기 프로그램(부트로더)가 저장
• 전원 인가 후
  • 컴퓨터는 부트로더 맨 앞 주소의 데이터를 불러옴
  • 부트로더는 디스크에서 메인 메모리로 데이터를 가져옴

• ROM
  

  

  • 읽기 기능이 없어 Chip select와 주소 입력만이 존재
  • 칩에 따라 read 입력이 있을 수도 있음
• RAM
  

  

  • ROM에서 read, write 신호 입력이 추가
  • chip select 입력이 맞지 않거나, read/write 신호가 모두 low인 경우 high-z상태로 사용되지 않는 상태가 됨

Hard Disk

• HDD의 구성 단위
  • Track : hdd에서 지름이 같은 하나의 동신원 구역
  • Sector : hdd를 중심을 기준으로 n등분했을 때 1개 구역
  • Cylinder : HDD는 여러 개의 판(platter)로 구성되는데, 플래터들의 같은 트랙의 집합을 실린더라고 칭한다.
• HDD의 데이터 저장 : 헤드가 자기장을 가하면 데이터가 1, 가하지 않으면 0으로 인식

Assiciative memory(CAM)

• 메모리 내용 자체가 주소 역할
• RAM 대비 고기이나, 탐색 시 시간이 매우 빠름

  

• CAM 동작
  • m개 word, n개 bit
  • Argument register에 데이터가 입력
  • 해당 데이터가 존재 시 Match register의 인덱스가 set
  • Argument register과 메모리 내용 사이에서 탐색할 범위를 Key register로 설정 (Masking)
  • 데이터를 쓸 때는 tag register가 사용 : 데이터의 저장 여부를 판단

Cache memory

• 캐시 메모리의 동작
  • CPU가 데이터를 필요로 할 때, 캐시로 먼저 접근
  • 캐시 데이터 존재시 읽음
  • 캐시에 데이터가 존재하지 않을 경우 메모리 접근
• hit ratio
  • CPU가 찾는 데이터가 캐시에 있을 확률
  • (1 - hit ratio) * main memory 접근시간 + cache memory 접근시간 = 평균 접근 시간
  • 반대어 : miss ratio(없을 확률)
• mapping
  • RAM 데이터를 캐시로 옮기는 과정
  • Associative mapping
    

    

    • CAM을 이용한 addressing - 주소 | data로 된 표 형태로 저장
  • direct mapping
    

    

    • 주소 필드의 일부를 cache memory 접근 시 사용
    • cache memory의 tag register과 주소 필드의 tag register를 비교하여 동일할 경우 데이터를 가져옴
    • 불일치 시 원래 캐시 정보를 메인메모리로 갱신하고, 새로운 메인메모리 정보의 tag와 데이터 갱신
  • set associative mapping
    

    

    • direct mapping의 개선
    • 캐시의 tag-data 표가 2중으로 존재
• replacement policy
  • 캐시 메모리의 용량이 제한되어 있기 때문에, miss로 인한 새 데이터 진입 시 갱신 알고리즘이 필요
  • LRU(Least Recently Used) : 가장 과거에 사용된 데이터가 갱신됨
  • FIFO : 가장 먼저 들어온 데이터가 갱신됨

• cache의 read/write 정책
  • CPU가 캐시 word를 읽을 때 : 메인 메모리에 접근 x
  • 캐시에 쓸 때 : 메인 메모리는 갱신된 데이터를 저장해야 함 (coherency problem)
    • write through
      • 캐시 업데이트시마다 메모리 갱신
      • 이동하는 데이터가 많아짐(traffic problem)
    • write back : 캐시에 replace 발생 시 메모리 갱신
  • cache initialize
    • 캐시 각 주소에는 valid, dirty의 2가지 bit가 할당
    • valid는 데이터의 가용성을, dirty는 데이터의 변형 여부(coherence problem 여부)를 나타냄
    • write-back 정책의 경우 dirty bit가 설정되어 있으면 갱신하게 됨

Virtual Memory

• 프로그램 실행 시 보조 장치(ex. HDD)의 데이터를 주 메모리에 적재 후 실행하게 됨
• 이때 주 메모리의 크기보다 큰 프로그램은 다 적재할 수 없게되는 문제가 존재
  • 보조 저장 장치의 Controller를 이용하여 저장소 주소를 주 메모리로 Mapping함
  • 캐시 - 주 메모리의 관계와 유사하게 동작
• 가상 메모리 존재 시 주소 space 크기는 실제 메모리 공간보다 크게 할당
  • 임베디드 등 가상메모리가 사용되지 않는 경우 주소필드와 메모리 영역은 동일

• page를 이용한 주소 매핑
  

  

  • 실제 메모리는 일정 크기의 block으로 분할
  • 가상 메모리 주소는 일정 크기의 page로 분할 = 프로그램 실행 시 page 단위로 나누어 메모리에 적재
  • virtual address = page number + page line

• virtual address 중 page number는 memory page table에 접근
  • page table의 주소로 접근하여 address를 반환
• virtual address의 line number와 mem.page table에서 반환받은 값을 합쳐 실제 메모리로 접근
• 실제 메모리가 할당 가능한 block 크기에 따라 memory page table도 갱신을 거쳐야 함(FIFO or LRU)
  • 경우에 따라 associative memory table을 이용하여 page / block을 대응시켜 mapping하기도 함

Memory management

• segment : 논리적으로 연관 있는 명령어나 데이터의 집합
  • 서브루틴, 데이터 배열, symbol, 프로그램 등
  • 세그먼트 관리 시 인증되지 않은 접근에서 보호할 필요 존재

    

• logical address는 segment, page, word로 구성됨
  • segment는 table을 거쳐 page와 합쳐짐
  • page table에서 block 위치를 탐색하여 word와 함께 실제 주소를 탐색
  • 최대 접근 가능한 메모리 주소는 page와 word 개수의 곱으로 나타남 $2^{pagebit}\times2^{wordbit}$

regularization

• Overfitting : regression 식의 feature 개수가 너무 많아지면, 학습 데이터에 대한 정확도는 높아지지만 새로운 데이터에 대한 정확도는 오히려 낮아지는 현상
  • feature 수를 줄이거나, regularization을 통해 완화
  • feature 수를 줄일 경우 보존할 feature를 선택해야 하는 문제가 존재 ( model selection algorithm )

• regularization
  • 모든 feature의 영향을 보존
  • parameter를 최소화하여 각 feature의 영향을 경감
• cost function $J(\theta)=\frac{1}{2m}\sum(H_\theta(x^i)-y^i)^2+\frac{\lambda}{2m}\sum\theta_i^2$
  • $\lambda$ : regularization parameter
  • $\lambda$가 커질수록 underfitting, 작아질수록 overfitting
  • 이처럼 학습이 아닌 실험적으로 찾아야 하는 값을 hyper-parameter라고 함
• normal eq. : $\theta = (X^TX+\lambda L)^{-1}X^Ty$

Model Evaluation

• Training / Test set : 데이터 중 일부는 학습에, 일부는 검증에 사용
• holdout validation : 데이터를 training / validation / test로 분리하여 학습
  • validation 데이터를 통해 모델을 최적화
  • 해당 모델을 test 데이터를 통해 학습 정도를 판별
• Bias vs Variance
  • Variance가 높을수록 모델의 degree, complexity가 높아짐
  • Bias가 높을수록 제대로 학습되지 않은 상태
• 오차에 대해
  • 모델 degree가 높을수록 train set의 cost는 감소하나, valid set은 감소하다가 일정 이상부터 오히려 증가
  • 큰 train / valid cost = Bias가 높다, underfitting
  • 큰 valid cost / 작은 train cost = Variance가 높다, overfitting
• 정규화 parameter $\lambda$에 대해
  • $\lambda$가 커질수록 train cost는 증가하고, valid 코스트는 감소하다 증가한다
  • valid cost가 크고, train cost가 작으면 variance가 큰 상태
  • train/valid cost가 모두 크면 bias가 큰 상태

• K-fold cross validation
  • 데이터를 K개로 분할
  • 이중 1개를 validation으로 선정하고, 나머지를 training set으로 선정
  • 모든 subset에 대해 돌아가며 학습 : subset 크기가 클 수록 train cost는 증가하고, valid cost는 감소
• learning curve
  • Bias가 높은 경우 : 일정 error 이하로는 학습되지 않음
  • 최적화된 경우 : 낮은 error로 학습되나 충분한 반복 필요
  • overfitting된 경우 : 최적 반복 지점에서 학습을 중단하지 않으면 valid cost가 역으로 높아질 수 있음

• Overfitting의 대처법
  • training set의 크기를 증가
  • feature 개수를 감소
  • regularization parameter를 증가
  • iteration 감소
• Underfitting 대처법
  • feature 개수 증가, 모델 degree 증가
  • regularization parameter 감소
  • iteration 증가

• norm : data 간의 거리 / 판정의 기준

Vector norm

• $\R^n$은 n차원 공간 내의 함수$\{(x_1, x_2, ..., x_n|x \in R\}$를 의미
• vector norm의 성질
  • $||\bold{x}||\geq0\ for\ all\ x\in\R^n$
  • x가 영벡터일 때만 $||\bold{x}||=0$
  • 모든 실수 $\alpha$에 대해 $||\alpha\bold{x}||=|\alpha|||\bold{x}||$
  • triangle inequality : $||\bold{x+y}||\leq||\bold{x}||+||\bold{y}||$
• Cauchy-Bunyakovsky-Schwarz Inequality
  • 벡터 x, y에 대해서
  • $x^ty=\sum^n_{i=1}x_iy_i\leq\{\sum x_i^2\}^{1/2}\{\sum y_i^2\}^{1/2}=||x||_2||y||_2$

• $l_2$ norm과 $l_\infty$ norm
  • 전자는 square norm, 후자는 max norm이라고 칭함
  • 선형대수에서 가장 보편적으로 사용되는 norm
  • $l_2$ norm : $||\bold{x}||_2=\{\sum_{i=1}^nx^2_i\}^{1/2}$
    

    

    • 2차원 실수 공간의 $l_2$ < 1 norm
  • $l_\infty$ norm : $||\bold{x}||_\infty=max|x_i|$
    

    

    • 2차원 실수 공간의 $l_\infty$ < 1 norm
• ex. 벡터 x = (-1, 1, -2)인 경우
  • $l_2$ norm = $\sqrt{6}$
  • $l_\infty$ norm = 2

• Cauchy-Bunyakovsky-Schwarz Inequality의 증명
  • 임의 벡터 x, y가 영벡터가 아닐 때
  • $0\leq||x-\lambda y||_2^2=\sum(x_i-\lambda y_i)^2$
  • 즉 $2\lambda\sum x_iy_i\leq\sum x_i^2 + \sum y_i^2=||x||_2^2+\lambda^2||y||_2^2$
  • $||x||_2>0,\ ||y||_2>0$이므로 $\lambda=||x||_2/||y||_2$로 가정하면 $2\sum x_iy_i\leq2||x||_2||y||_2$

• norm 간의 비교
  • $||x||_\infty\leq||x||_2\leq\sqrt{n}||x||_\infty$ ( n : 차원 )
  • 증명 : $||x||_\infty=|x_j|^2\leq\sum x_i^2=||x||_2^2 \\ ||x||_2^2\leq nx_j^2=n||x||_\infty^2$

Matrix norm

• vector 계산에서 행렬은 변환을 담당(X 공간에서 Y공간으로의 이동)
  • function : 벡터 or 실수 > 실수
  • operator : 벡터 > 벡터
• Matrix norm은 vector norm과 유사한 특성을 보유
  • $||\bold{A}||\geq0$
  • A가 영행렬일 때만 $||\bold{A}||=0$
  • 모든 실수 $\alpha$에 대해 $||\alpha\bold{A}||=|\alpha|||\bold{A}||$
  • triangle inequality : $||\bold{A+B}||\leq||\bold{A}||+||\bold{B}||$
  • $||\bold{AB}||\leq||\bold{A}||||\bold{B}||$

• Matrix Norm : $||A||=max_{||x||=1}||Ax||$
• Natural(Mmatrix) Norm
  • 영벡터가 아닌 임의 벡터 z가 있을 때, unit vector $x=z/||z||$로 정의
  • 즉 $||A||=max_{z\not ={0}}\frac{||Az||}{||z||}=max_{||x||=1}||Ax||$
• Matrix norm은 vector norm에 종속되어 결정

• A가 n x n크기의 행렬일 때, $||A||_\infty = max\sum|a_{ij}|$
  • $||A||$는 행렬 A와 unit vector 사이의 곱이므로, 무한 차원의 norm은 행의 절댓값 합 중 최댓값으로 나타나게 된다.

LU decomposition

• $2x_1+x_2=1,\ x_1+2x_2=3$의 방정식 가정
  • $\begin{bmatrix} 2\ 1:1\\ 1\ 2:3 \end{bmatrix}$ : augmented matrix
  • x계수 행렬을 system matrix라고 함
• Gauss Elimination : 계수 소거
  • $\begin{bmatrix} 2\ 1:1\\ 0\ \frac{3}{2}:\frac{5}{2} \end{bmatrix}$
  • 2열에 1열 / 2한 것을 빼서 계산
  • $x_2=5/3$, $x_1=-1/3$
• $Ax=b$를 Gaussian Elimination을 통해 $Ux=b'$으로 변환
  • $U=\begin{bmatrix} a\ b\\ 0\ d \end{bmatrix}$꼴의 행렬

• $Ax=b_1,\ Ax=b_2,\ Ax=b_3, ...$의 행렬식을 푼다고 하면 각 행렬마다 Gauss Elimination이 적용되어야 함

  • Lower - Triangle Matrix L : $L=\begin{bmatrix} a\ 0\\ c\ d \end{bmatrix}$
  • Gauss-Elimitation 연산을 기억하는 효과
  • $A=LU$

• LU Decomposition

  • $A = \begin{bmatrix} 2\ 1\\ 1\ 2 \end{bmatrix} = LU$
    • $U = \begin{bmatrix} 2\ 1\\ 0\ \frac{3}{2} \end{bmatrix}$
    • $L = \begin{bmatrix} 1\ 0\\ k\ 1 \end{bmatrix}$
      • k = 상수항 제거를 위해 Gauss Elimination에 적용한 계수
  • $Ax=b\rarr LUx=b$

• Gauss Elimitnation은 계수 행렬 A에서 항 하나가 제거된 Lower Matrix L로 변환하는 과정을 거침

• LU-Decomposition은 계수행렬 A를 L과 U의 곱으로 변환

  • 우항이 바뀌어도 LU식은 변화 없음

• m x n 행렬의 LU decomposition
  • i행 j열 위치의 값을 $a_ji$라고 할 때,
  • j번째 행의 원소 $E_j$의 값을 $E_j-m_{j1}E_1$로 바꿔준다 ($m_j1=\frac{a_j1}{a_11}$)
  • j번째 행의 원소 $E_j$의 값을 $E_j-m_{j2}E_1$로 바꿔준다
  • 1열의 모든 행에 대해 위 계산을 반복한 결과 행렬이 U행렬
  • 위 식에서 계산한 계수 m으로 이루어진 행렬이 L행렬이다.
• Permutation
  • Gauss Elimination 연산이 불가능한 경우 계수 행렬의 열을 맞바꿈
  • P = (a, b) : 바꿀 두 행 a, b를 지정
    • ex. P = (1, 2) (2, 4)의 경우, 1 - 2행을 바꾼 후 2 - 4행을 바꿈
    • $P \begin{bmatrix} 0\ 1\ 0\ 0\\ 0\ 0\ 0\ 1\\ 0\ 0\ 1\ 0\\ 1\ 0\ 0\ 0 \end{bmatrix}$
  • PA = LU의 관계식을 만족
  • $A = P^{-1}LU = P^tLU$

Positive definitive

• n x n 행렬 A가 있을 때,
  • $|a_{ii}|\geq\sum^n_{j=1, j\not ={i}}|a_{ij}|$이면 diagonally dominant 하다고 표현
  • $|a_{ii}|>\sum^n_{j=1, j\not ={i}}|a_{ij}|$ 이면 strictly digonally dominant
• $det(A)\not ={0}\lrArr A^{-1}\ exist$
  • determinant가 0이 아님을 증명하는 계산 과정은 복잡
  • 그 대신 (strictly) diagnally dominant이면 $A^{-1}$이 존재하다는 것을 이용
  • $diag.\ dominant A\larr A^{-1}\ exist$
  • $strictly\ diag.\ dominant A\lrarr A^{-1}\ exist$ : non-singluar

• 0이 아닌 벡터 x에 대해
  • $x^tAx>0$이면 A는 positive definitive하다고 정의
• positive definitive할 경우
  • 역행렬이 존재
  • 모든 대각 성분은 양수
  • 행렬 내 임의 값의 최대값보다 대각 성분의 최대값이 더 큼
  • i행 j열에서 $(a_{ij})^2<a_{ii}a_{jj}$

• n x n 행렬 내에는 n개의 leading submatrix가 존재
  • leading submetrix : 행렬의 1,1 원소를 공통으로 갖는 1 x 1, ..., n x n 크기의 대칭행렬
  • 대칭행렬 A의 leading submatrix가 모두 행렬식이 양수인 경우, A는 positive definitive

Euler's method

• 가장 단순한 미분법
• Initial value problem
  • $\frac{dy}{dt}=f(t,y),\ a\leq t\leq b, y(a)=\alpha$
  • [a,b] 범위를 n등분 : $t_i=a+ih,\ i=0,1,2,...,n$
  • $h=(b-a)/n=t_{i+1}-t_i$를 step size라고 정의
• euler's method 유도를 위한 taylor's theorem
  • $y(t_{i+1})=y(t_i)+(t_{i+1}-t_i)y'(t_i)+\frac{(t_{i+1}-t)^2}{2}y''(\zeta_i)\ (t_i\leq\zeta\leq t_{i+1})$
  • step size 공식에 의해 $y(t_{i+1})=y(t_i)+hf(t_i, y(t_i)) + \frac{h^2}{2}y''(\zeta_i)$

• Euler's method
  • $w_i\simeq y(t_i)$로 정으
  • $w_0 = \alpha$
  • $w_{i+1}=w_i+hf(t_i, w_i)$
• ex. h = 0.5, y(0)=0.5, $y'=y-t^2+1$
  • $w_0=y(0)=0.5$
  • $w_1=w_0+0.5(w_0-0^2+1)$
  • $w_2=w_1+0.5(w_1-(0.5)^2+1$
• $w_{j+1}=w_j+hf(t_j, w_j)$ : worward euler method
  • h가 커지면 발산할 위험이 있음
• $w_{j+1}\simeq w_j + hf(t_{j+1}, y_{j+1})$ : backward euler method
  • $w_{j+1}$을 풀어야 하나, stable한 장점이 있음

• Runge-Katta method (order 2)
  • $\int^{t_{j+1}}_{t_j}y'dt=\int^{t_{j+1}}_{t_j}f(t, y(t))dt\\\rarr y_{j+1}-y_j\simeq \frac{h}{2}[f(t_j, y_j) + f(t_{j+1}, y_{j+1})]$ : Implicit
  • Explicit : $y_{j+1}-y_j\simeq \frac{h}{2}[f(t_j, y_j) + f(t_{j+1}, \hat{y_{j+1})}]$
    • $y_{j+1}\simeq\hat{y_{j+1}}=y_j+hf(t_j, y_j)$
• Runge-Katta method (order 4)
  • Implicit : $y_{j+1}-y_j = \frac{h}{6}[f(t_j, y_j) + 4f(t_{j+1/2}, y_{j+1/2})+f(t_{j+1}, y_{j+1})]$
  • Explicit : $y_{j+1}-y_j = \frac{h}{6}[f(t_j, y_j) + 2f(t_{j+1/2}, \hat{y_{j+1/2}})+2f(t_{j+1/2}, \hat{\hat{y_{j+1/2}}})+f(t_{j+1}, \hat{y_{j+1}})]$
    • $\hat{y_{j+1/2}}=y_j+\frac{h}{2}f(t_j, y_j)$
    • $\hat{\hat{y_{j+1/2}}}=y_j+\frac{h}{2}f(t_j, \hat{y_j})$
    • $\hat{y_{j+1}}=y_j+hf(t_j+\hat{\hat{y_{j+1/2}}})$