[자동제어] 3. Dynamic Response

3. Dynamic Response

1. Laplace transform

• 미분 방정식의 풀이를 위해 사용
• $\mathcal{L}\{{f(t)}\}=\int_0^\infty f(t)e^{-st}dt=F(s)$
  • 시간 영역의 함수 f(t)를 주파수 영역의 함수 F(s)로 변환
  • $s=-\sigma\pm jw$
  • $jw$ : f(t)의 주파수
  • $\sigma$ : 진폭의 감쇄
  • Fourier Transform : $s=\pm jw$에 대한 Laplace Transform
• Laplace Transform Property
  • $\mathcal{L}\{f(t)\}=F(s)$
  • $\mathcal{L}^{-1}\{F(s)\}=f(t)$ (inverse L.T.)
  • $\mathcal{L}\{kf(t)\}=kF(s)$
  • $\mathcal{L}\{f_1(t)+f_2(t)\}=F_1(s)+F_2(s)$
  • $\mathcal{L}[\frac{df(t)}{dt}]=sF(s)+f(0)$
  • $\mathcal{L}[\frac{d^nf(t)}{dt^n}]=s^nF(s)-s^{n-1}f(0)-s^{n-2}f'(0)-...-f^{n-1}(0)$
  • $\mathcal{L}[\int^t_0f(\tau)d\tau]=\frac{1}{s}F(s)$

---

2. Inverse Laplace Transform

• $F(s)=\frac{b_1s^m+b_2s^{m-1}+...+b_{m+1}}{s^n+a_1s^{n-1}+...+a_n}=K\frac{\Pi_{i=1}^m(s-z_i)}{\Pi_{i=1}^n(s-p_i)}$
  • 실제 존재할 수 있는 Transfer function에 대해 $n\geq m$
  • $z_i$ : 함수의 영점(zero)
  • $p_i$ : 함수의 극점(pole)
  • Partial Fraction : $F(s)=\frac{C_1}{s-p_1}+\frac{C_2}{s-p_2}+...+\frac{C_m}{s-p_n}$
    • $C_1=(s-p_1)F(s)|_{s=p_1}$

---

3. Final-value Theorem

• Laplace Transform을 이용, 시간이 무한히 흘렀을 때의 시스템의 최종값 계산
• sY(s)의 모든 극값이 좌반면 (s < 0)에 존재하는 경우
  • $\lim_{t\rarr\infty}y(t)=lim_{s\rarr0}sY(s)$
• sY(s)의 모든 극값이 좌반면에 존재한다
  • = 분모의 식이 (s+a)(s+b)(s+c)...꼴로 표현
  • 이는 $y(t)=A_0+A_1e^{-at}+A_2e^{-bt}...$, 즉 0으로 수렴하는 식으로 표현
  • 만약 우반면에 존재하는 극값이 존재할 경우 y(t)는 무한으로 발산
• DC Gain
  • 임의 시스템의 Transfer Function G(s)와, 입력U(s), 출력Y(s) 가정
  • $G(S)=\frac{Y(s)}{U(s)}$
  • DC gain = $lim_{t\rarr\infty}\frac{y(t)}{u(t)}=lim_{s\rarr0}G(s)$ : 입력과 무관한 시스템 고유의 특성

---

4. System Modeling

• 시스템의 신호 흐름을 표시
  

  

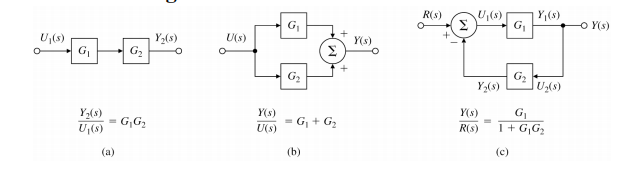
1. 직렬 결합
   • G1, G2의 두 시스템이 같은 선에 위치할 경우
   • 시스템은 G1, G2의 곱으로 표시
2. 병렬 결합
   • 분기점을 기준으로 G1, G2가 나눠진 후 다시 결합
   • 시스템은 G1, G2의 합으로 표시
3. 피드백
   • $\frac{진행\ 방향}{1\mp feedback\ loop}$
   • Unit negative feedback : feedback block이 1인 Block diagram
     • 출력 신호가 온전히 input으로 들어오는, 이상적인 feedback

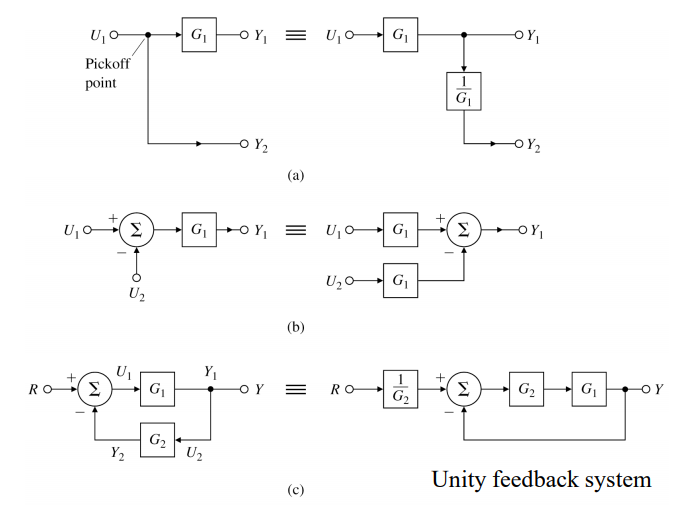
• 분기점(pickoff point) 이전의 분기신호를 분기점 이후로 옮기면, 중간에 있는 block의 역수인 block을 곱하여 배치한다.
• 신호가 합쳐진 뒤 있는 block은 합쳐지기 전 각각 신호에 block이 있는 회로와 동일
• feedback을 전향경로와 동일한 선에 배치할 때, feedback point 이전에 피드백 block의 역수인 block을 배치한다.

---

5. Effect of Pole Location

• 시스템의 전달함수가 $H(s)$일 때
  • $H(s)=\frac{b(s)}{a(s)}=\frac{b_1s^m+b_2s^{m-1}...+b_ms+b_{m+1}}{a_1s^n+a_2s^{n-1}...+a_ns+a_{n+1}}=K\frac{\Pi_{i=1}^m(s-z_i)}{\Pi_{i=1}^n(s-p_i)}$
  • pole : $H(s)$가 $\infty$가 되는 값들 ($a(s)=0$)
  • zero : $H(s)$가 0이 되는 값들 ($b(s)=0$)
• Impulse response
  • impulse function : let $u(t)=\delta(t)$, $U(s)=1$
  • 시스템 $H(s)$의 impulse 입력에 대한 출력
  • $Y(s)=H(s)U(s)=H(s)\cdot1=H(s)$
    출력 $y(t)=\mathcal{L}^-1\{H(s)\}=h(t)$
    • 크기가 1인 순간 출력에 대한 응답이므로, 시스템 자체의 고유한 response이기 때문에 impulse response를 natural response라고도 함.

---

• ex. 1st order pole
  • $H(s)=\frac{1}{s+\sigma}$
  • impulse response $h(t)=exp[-\sigma t]$
  • $\sigma$가 양수일 때 시간에 따라 response가 0으로 수렴하며, 이를 stable하다고 표현
    • $H(s)$의 pole이 음수(s-plane의 좌반면)일 때 시스템은 stable한 상태가 됨
  • 1차 시스템의 time constant
    • 시스템 response가 $\frac{1}{e}$가 되는 시간 $\tau$
    • time constant가 클 수록 응답의 속도가 빠름

---

• ex. 2개의 complex pole을 갖는 시스템

  • pole $s=-\sigma\pm jw_d$
  • $H(s)=\frac{w_n^2}{(s+\sigma)^2+w_d^2}=\frac{w_n^2}{s^2+2\zeta w_ns+w_n^2}$
  • $\zeta$ : damping ratio (속도에 의한 감쇠)
  • $w_n$ : damping이 없을 때 진동 주파수
  • $w_d$ : damping이 있을 때 진동 주파수 ($w_d=w_n\sqrt{1-\zeta^2}$)
  • impulse response $h(t)$는 지수함수와 삼각함수의 곱으로 표현됨

• s-plane expression
  

  

  • pole $s=-\sigma\pm jw_d$
  • $w_n^2=w_d^2+\sigma^2$
  • $\sigma=\zeta w_n$에서 $\zeta=\frac{\sigma}{w_n}=sin\theta$
    $\theta=sin^{-1}\zeta$

• 2차 시스템의 impulse response

  • $H(s)=\frac{w_n^2}{(s+\sigma)^2+w_d^2}$
    ( $\sigma=\zeta w_n$, $w_d=w_n\sqrt{1-\zeta^2}$)
    $=\frac{w_n^2}{(s+\zeta w_n)^2+w_n^2(1-\zeta^2)}$

  • $(L.T.)e^{-at}sin(bt)=\frac{b}{(s+a)^2+b^2}$
    $\frac{w_n}{\sqrt{1-\zeta^2}}\frac{w_n\sqrt{1-\zeta^2}}{(s+(\zeta w_n)^2+w_n^2(1-\zeta^2)}$
    $a=\zeta w_n$, $b=w_n\sqrt{1-\zeta^2}$

  • $\therefore h(t)=\frac{w_n}{\sqrt{1-\zeta^2}}e^{-\zeta w_nt}sin[(w_n\sqrt{1-\zeta^2})t]$

  • 2차 시스템의 impulse response는 undamped natural frequency $w_n$과 damping ratio $\zeta$에 의해 결정

    • $\zeta=0$ : 감쇄 없이 진동
    • $\zeta<1$ : 감쇄하면서 진동 (underdamped)
    • $\zeta=1$ : 진동 없는 감쇄 (Critical damped)
    • $\zeta>1$ : 목표값보다 과하게 감쇄되어 벗어남 (overdamped)

  • damping ratio $0\leq\zeta\leq1$ 가 증가 > 실제 주파수 감소

  • damping ratio가 증가 > 허수축에서 pole이 멀어짐 > $\theta$ 증가

---

6. Step Response

• 임의 시스템 $H(s)$의 unit step $u(t)$에 대한 응답
• unit step의 laplace transform $U(S)=\frac{1}{s}$
• step response는 0에서 시작해서크기 1을 향해 진동하면서 수렴
• rising time ($t_r$) : 목표값의 10%에서 90%까지 상승하는 시간
• peak time ($t_p$) : 시작점에서 peak점에 도달할 때까지의 시간
  • step response : $Y(s)=\frac{w_n^2}{(s+\sigma)^2+w_d^2}\frac{1}{s}$
  • $y(t)=1-e^{-\sigma t}[cosw_dt+\frac{\sigma}{w_d}sinw_dt]$
  • peak time에서 응답곡선 기울기 = 0
  • $\dot{y}(t)=e^{-\sigma t}[\frac{\sigma^2}{w_d}sinw_dt+w_dsinw_dt]=0$
  • $w_dt=\pi$인 시간이 peak time : $t_p=\frac{\pi}{w_d}$
  • peak time은 damped natural frequency의 함수
• Overshoot ($M_p$) : peak값과 목표값의 차이
  • $M_p=1-y(t_p)=1-(1+e^{-\sigma\pi/w_d})=exp[-\sigma\pi/w_d]$
  • $\sigma=\zeta w_n$, $w_d=w_n\sqrt{1-\zeta^2}$이므로
    $M_p=exp[-\pi\zeta/\sqrt{1-\zeta^2}]$
  • overshoot는 damping ratio의 함수
• settling time : 응답곡선이 목표값의 $\pm1\%$내에 도달하는 시간

---

• Controller Design
  • 2차 step response $Y(s)=\frac{w_n^2}{(s+\sigma)^2+w_d^2}\frac{1}{s}$ 의 주요 parameter :
    rising time, peak time, overshoot, settling time
  • settling time
    • 응답 y(t)=0.01이 되는 시간
    • $\sigma\geq\frac{4.6}{t_s}$
  • rising time
    • 목표값의 10%에서 90%까지 상승하는 시간
    • $w_n\geq\frac{1.8}{t_r}$

---

7. Stability

• Routh's Stability Criterion

  • 임의 시스템의 pole이 모두 s-plane 좌반면에 존재하면 시스템은 stable

  • n차 시스템 $a(s)=s^n+a_1s^{n-1}+a_2s^{n-2}+...+a_n$의 안정도 판단

  • 안정 시스템의 필요조건 : 모든 계수 $a_1$~$a_n$이 양수

  • 안정 시스템의 필요충분조건 : routh array의 1번 열이 모두 양수

    

  • special case

    • 계수의 행이 최소공배수를 갖는 경우 최소공배수로 나누어 표현 가능 (부호는 변경할 수 없음)
      • ex. 행 계수가 3, 24, 96, 192인 경우 3으로 나누어 1, 8, 32, 64로 표현 가능
    • 계산한 계수 값이 0인 경우 : $\epsilon(=0^+)$로 대체하여 array 완성 후 부호 비교
    • array 중 a번째 행이 모두 0이 된 경우
      • a+1행 계수로 보조방정식 구성
      • 이 식을 미분한 계수로 0이 된 행 대체
      • ex. $s^1$행이 0, $s^2$행이 3, 12인 경우
        • $a_1(s)=3s^2+12s^0$
        • $\frac{da_1(s)}{ds}=6s$
        • 즉 0이 된 $s^1$행의 1열 계수는 6
      • a+1행부터 시작하는 보조 routh-array 추출
        • 보조 routh-array에서의 RHP = LHP, 남는 근은 허수축 위에 존재
      • routh-array에서 a+1행 위의 계수로 보조방정식 외 나머지 pole 위치 판단