Documentation

• Combinational Logic

  • 다수의 입/출력의 조합 : 진리표가 매우 복잡하다

• Documentation Standrads

  • 정확하고, 제조 가능하며, 유지보수가 가능한 디자인임을 보증
  • 구성요소
    • 스펙
    • 블록 다이어그램 : informal spec
    • schematic diagram : 공식적 스펙
      • 전기적 소자 연결, IC 타입, 핀 구성 등
    • timing diagram : 시그널 순서, 시그널 간 딜레이
    • logic device description : 논리식, 진리표, HDL 혹은 C언어로 작성됨
    • circuit description : 앞서 설명한 내용으로 설명하기 애매한 내용들

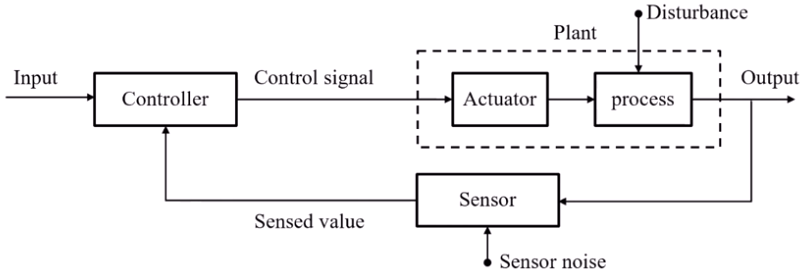
• Block Diagram : 입/출력, 내부 신호 전달
  

  

  • 작성 시 과하게 상세하거나, 애매하게 작성하지 않도록 한다.

• Signal Name

  • 변수 이름의 적절한 지정은 회로 이해에 큰 도움이 된다.
  • Go, Pause, Ready, Error 등등...
  • 신호가 asserted : 신호가 active 상태이다
  • 신호가 deasserted/negated : 신호가 active 상태가 아니다

• Bubble-to-Bubble Logic Design
  

  

  • 일반적으로 Inverting Gate가 Non-Inverting Gate보다 빠르다
  • 신호가 전달될 때 Bubble끼리 전달되도록 한다.

• Drawing Layout

  • 손으로 그리는 경우, 연결점에 dot(●) 표시를 한다.

  • 프로그램을 통해 그리는 경우, T자 접점은 허용되나, 십자 교차로 연결을 표시하는 것은 금지된다(몇몇 SW에서는 dot표시가 불가)

  • Flat Schematic Structure
    

    

    • 복잡한 회로 구성에 사용되는 방식 중 하나
    • 장점 : 회로의 부분을 각 페이지에 나누어 표시하여 모든 회로를 한 눈에 볼 수 있음
    • 단점 : 회로가 복잡해 보인다.

  • Hierarchical(구조적) Schematic Structure
    

    

    • 회로 간의 연관관계를 표시
    • 장점 : 회로 구성이 비교적 간단하게 보임
    • 단점 : 한 눈에 보기 힘듦

• 버스 : 2개 이상의 연관된 신호의 조합

Circuit Timing

• Timing Diagram : 시간적 제약의 표현을 위해 신호 간의 timing을 나타낸 것

• data 신호에 대해서, timing diagram은 data 신호가 0인지, 1인지 표시할 필요가 없다. 대신 신호가 겹치는 표시를 이용하여 신호 변화를 표시한다.
  

  

• data bus에 대해 data[7:0]과 같은 식으로 표기하며, 버스 내 신호는 항상 같은 시간 timing 을 갖는다.
  

  

• 모든 회로는 H->L, L->H에 대해 서로 다른 Propagation Delay를 갖는다.

• 회로 구성시 Propagation Delay는 더 나쁜 값을 고려하여야 한다.

Programmable Logic Devices

• PLD : 사용자가 제한된 범위 내에서 원하는 기능을 구현 가능한 device

• PLA(Programmable Logic Arrays) : 2-Level And-Or Device

  • Minterm Expressions : AND 조합이 논리합으로 나타나는 논리식을 표현
  • PLA device : n x m PLA with p product terms
    • n : 입력
    • m : 출력 = p개 입력을 갖는 OR gate 개수
    • p : product 식의 개수 = 2n개 입력을 갖는 AND gate 개수
    • PLA 입력 연결을 연결하지 않으면 1이 됨
    • PLA 입력을 모두 연결하면 0이 됨
    • PLA 출력을 연결하지 않으면 0이 됨

• PAL(programmable Array Logic) : 최근 가장 많이 사용되는 PLD

  • OR array가 고정된 채, And Array를 설정 가능
  • bidirectional i/o pin : 입/출력이 한 핀에서 사용 가능(내부 회로에서 지원 시)
  • PAL16L8 : 10개의 입력, 6개의 I/O핀, 2개의 출력핀
    • 최대 16개 입력, 8개 출력까지 지원 가능
  • GAL : Generic Array Logic devices
    • 출력단 XOR 게이트의 한쪽 단자를 GND와 fuse하여 출력 신호를 통과시키거나, high로 만들어 invert 신호를 출력할 수 있게 한다.
  • CPLD(complex PLD) : 다수의 PLD를 각 PLD에 원하는 기능을 구현 후 조합한 것
  • EEPLD(Electrically Erasable PLD) : 한번 프로그램 후에도 지우고 다시 재프로그래밍이 가능한 PLD

Decoder / Encoder

• Decoder
  • code를 푸는 회로
  • 코드, n개 입력, m개 출력으로 구성되어, 출력 포트 중 하나의 포트로만 신호가 출력된다.
    

    

  • 7-segment decoder
    • 7-segment : 7개 LED로 문자/숫자를 표시 가능한 display
      

      

    • 74x49 seven segment decoder를 이용하여 4-bit 입력을 7-segment 출력으로 변환
      

      

    • 위 진리표는 0~9 숫자만을 출력, 점선부분은 don't care terms
• Encoder
  • 코드르 만드는 회로
  • ex. $2^n$ to n binary encoder : $2^n$개 숫자를 n-bit 이진수로 변환

    

  • priority encoder : 입력에 우선순위가 존재
    • 기존 encoder의 경우 I0 입력의 floating 문제
    • 또한 비정상 출력이 존재 : I2, I4가 동시에 1이 되면 2진수 110-비정상 출력

      

    • GS_L : EI_L이 on(0)이면서 우선순위에 맞게 입력될 때 on
    • EO_L : EI_L이 on이면서 입력 없을 때 on
    • GS_L과 EO_L은 다수 74148 조합 시 사용

Tri-state devices

• 0, 1이 아닌 제3의 상태(Hi-Z)를 만들어 줌
  

  

• EN이 on일 때만 입력이 출력으로 전달되는 특성을 이용, 버스 출력에 활용 가능하다.
  

  

• dead time : low/high에서 Hi-z로 변하는 시간을 반대로 가는 시간보다 짧게 만들어 버퍼 신호 간 충돌을 막는다.
• 74245 transceiver : Tri-state buffer를 반대 방향으로 교차하여 방향 신호에 따라 데이터가 통신할 방향을 지시

  

Multiflexer(MUX)

• 입력 신호 중 원하는 신호를 선택하여 출력
• ex. 74151 8x1 multiplexer truth table

  

Demultiplexer(DeMUX)

• 입력 신호를 원하는 경로로 출력(Mux의 반대역할)
  

  

XOR gate / parity circuit

• XOR ($X = A\oplus B$) : 두 입력이 다를 때 1
• XNOR ($Y = A\odot B$) : 두 입력이 같을 때 1
• XOR parity gate
  • parity check
    • 신호 전송시 오류를 검출하는 방법
    • 오류 수정은 불가
    • 2진수 신호의 1 개수를 계산하여 even/odd parity에 따라 1의 개수가 짝/홀이 되도록 parity bit를 추가한다.
    • ex. even parity, 110 입력인 경우 parity bit=0
  • 입력을 모두 XOR하면 입력에서 1의 개수가 홀인지 짝인지 확인 가능
    • $1\oplus1\oplus0 = 0$

• ex. 에러 검출 회로
  

  

• 입력이 1110000일 때

1. write가 enable되면 메모리에 D1-D7이 저장
2. 이 때 74280(parity generator)가 xor 회로로 입력의 1 개수를 계산 (odd=1)

• write시에 I입력은 항상 0

3. read가 on일 시 74541 tri-state buffer가 enable되어 메모리 신호를 출력
4. 이때 저장된 PIN은 POUT을 통해 다시 74280으로 전송 (I = RD * POUT = 1)
5. 이 신호로 다시 74280이 parity check, odd 신호는 0이 됨(RP 포함, 1 111 0000)
6. 만약 read 중 8bit 신호 중 하나가 수정된 경우 odd가 1이 되면서 ERROR 신호가 on이 됨(ERROR = RD * ODD)

• Hamming Code
  • 오류 위치를 검출하고 1bit 오류에 대해 자기정정이 가능한 코드
  • n개 데이터에 k개 parity bit를 더하여 만들어짐
  • 패리티 비트는 $2^n(n=0,1,...)$번째 비트에 위치한다.
  • 데이터 비트 수는 $2^{k-1}-k-2\leq n\leq2^k-k-1(k\geq3)$의 공식을 따른다(k=2일 때 data bit = 1)

Arithmatic and Logic Unit(ALU)

• Comparator : 비교기
  • XOR 게이트를 사용, 두 입력이 같은지 확인
    

    

• 74x85 comparator
  • AGTBOUT : A가 B보다 크거나, AGTBIN 신호에 1이 전달되면 on
  • AEQBOUT : A와 B가 같으면서 AEQBIN에 1이 전달되면 on
  • ALTBOUT : A가 B보다 작거나, ALTBIN에 1이 전달되면 on
    

    

  1. 왼쪽 7485에 AEQBIN에 on(5V)신호를 전달하였고 A,B가 0101로 동일하므로 다음 7485에 AEQB on 전달
  2. 가운데 7485 역시 동일하게 AEQB on 전달
  3. 오른쪽 7485는 A가 1001, B는 1000으로 A가 B보다 더 크므로 AEQBOUT은 0, AGTBOUT에 1로 출력
• Half Adder
  • 1bit 숫자 2개를 더한다
  • 합과 Carry out을 각각 출력
  • 아래 자리수에의 올림인 Carry in은 더해지지 않음
• Full Adder
  • 더할 값 + 아래 자리수에서 올림의 합 계산
  • 자리수 올림되면 Carry out으로 출력
  • Ripple Adder
    

    

    • 전가산기 다수를 조합하여 여러 자리 수의 덧셈 구현
    • Carry in-out 전달 시간으로 인해 속도가 느림
  • Carry Lookahead Adder(자리올림 예측 가산기)
    • 생성(g) : carry out의 발생 여부
    • 전달(p) : carry in이 1일 경우, 덧셈의 결과가 carry out되는지 여부
    • $g = X_i * Y_i$
    • $p_i = X_i+y_i$(둘 중 하나만 1이면 carry in 발생시 carry out이 발생되므로)
    • $S = X \oplus Y \oplus C_{i}$
    • $C_{i} = g_{i-1} + p_{i-1} + C_{i-1}$
      

      

    • 구조가 복잡하여 4bit 이상으로는 잘 사용하지 않음(4bit CLA를 여러개 조합함)
• ALU
  • 산술, 논리 연산이 가능한 회로
  • 74181 : 입력과 4-bit 선택에 따라 다른 연산 결과가 나타남
    

    

한빛미디어의 나는 리뷰어 2020에 선정되어 도서를 지원받아 작성한 글입니다.

  C언어는 최근에는 파이썬의 등장으로 입문용 언어에서 조금 밀린 감도 있고, 웹/앱 프로그래밍에서야 존재를 잘 느끼기 힘들지만 임베디드와 리눅스 쪽에서는 아직도 꾸준히 쓰이고 있다. 나온지 20년?도 더 된 만큼 새로운 언어로 대체하고자 하는 움직임도 계속 있지만 한동안은 그 위치를 굳건히 하지 않을까 싶다.

  '알쏭달쏭 C언어 180제'(시바타 보요 외 1인 저, 안동현 옮김)은 Hello, World! 부터 시작하여 파일처리까지 13강에 걸쳐 180개 문제를 풀어보며 C언어 실력을 향상시킨다! 라는 취지로 나온 책이다. 처음 제목만 봤을때는 문제풀이인가? 라는 느낌이었는데, 책을 펼쳐보니 생각보다 괜찮은 책이었다고 생각한다.

  이 책의 장점이라면 그 구성에 있다고 생각한다. 많은 책들이 이론을 먼저 접하고 예제를 뒤에 푸는 방식으로 되어 있지만, 이 책은 사실상 예제를 먼저 풀어보고 그 예제에 사용된 이론을 짚어가는 느낌이다(문제집보다는 참고서? 라는 느낌이다...). 한 문제 단위로 실습을 진행하면서 이론을 짚어가니 단계적으로 진행하는 느낌도 좋고 무엇보다 프로그래밍은 직접 쳐 봐야 실력이 된다고 생각하기 때문에 이런 방식의 내용 전개가 마음에 들었던 것 같다. 

  뿐만 아니라 각 단원 사이에 실전 문제 파트를 배치해서 코드 외에 이론적인 부분을 보충할 수 있게 해놓은 점도 괜찮았다고 생각한다. 빈칸채우기나 제시된 코드의 동작 방향을 예측해보게 하는 식으로 일종의 쪽지시험같은 느낌으로 구성을 해 두었다.

  아쉬운 점이라면 아예 프로그래밍에 처음 손을 대는 사람에게는 살짝 걸릴 수 있는 점이, 많은 프로그래밍 입문서의 예를 보면 적어도 IDE나 편집기를 깔아보는 것부터 시작하는데 이 책의 경우 그 부분이 존재하지 않는다. 작가의 말에 Dev C++ 에디터를 추천한다는 말 정도뿐인데, 이 부분도 조금 보충이 되었다면 좋지 않았을까 싶다.

  자바/C에 이어 앞으로 파이썬도 출간될 예정이라고 하는데, 파이썬은 인터넷에 있는 점프투파이썬과 병행하면 확실히 기초 형성에 도움이 되지 않을까 싶다. 뿐만 아니라 이런 문제구성이라면 자료구조/알고리즘에 상당히 좋은 내용 구조라고 생각하는데 언젠가 볼 수 있길 기대해보고 싶다.

https://www.aladin.co.kr/shop/wproduct.aspx?ItemId=217416952

위 링크에서 구매하실 수 있습니다.

1. Automatic control

1. Open-loop control
   • 출력값을 측정하지 않는 시스템
   • 입력 - [Controller] - 제어값 - [Plant : Actuator - process] - 출력
   • Plant에는 외란(disturbance)가 가해진다.
   • 외란에 대한 feedback이 없으므로 input에 대한 오류가 생긴다. 반복할 수록 이는 누적된다. 결국 원하는 signal과 완전히 다른 값을 갖게 된다.

2. Closed-loop control
   • 센서를 이용하여 출력값을 측정하여 그 값을 control signal 결정에 사용한다
   • feedback control이라고도 한다.
   • 조절부의 output을 센서로 측정, 이 값을 feedback하여 controll signal 결정에 활용한다.
   • 목표하는 output과, 실제 output 간 차이를 측정하여 이를 보상한다.
   • 센서 역시 하나의 시스템이므로, 노이즈가 포함될 수밖에 없으나, output과 유사한 결과를 나타내므로 추정에 활용할 수 있다.

• block diagram : 시스템 구성 요소를 블록으로, 신호의 흐름을 화살표로 표시하여 시각화한 것

• Closed-loop system의 값 설정

  • input : 원하는 값
  • Controller : 목표값에 비례하는 입력신호(control signal) 발생
  • Plant : 제어요소 = 조절부(Controller) + 조작부(Actuator)
  • Controller : control signal을 Actuator로 전달
  • Actuator : actuator 신호를 출력
  • Disturbance : 제어값을 교란시키는 외부 신호

• Controller 설계 시 고려사항

  1. Command Following : Output이 Input을 잘 따르는가?
  2. Disturbance Rejection : 외란을 얼마나 잘 제거하는가?
  3. Insensivity to sensor noise : 센서 노이즈에 덜 민감한가?
  4. Insensivity to Modeling Error : 수학적 모델링 에러에 덜 민감한가?

0. Notation

• 랜덤변수는 대문자로 표기 ex) W, X, Y, Z, ....
• 랜덤 변수의 값은 소문자로 표기 ex) w, x, y, z...

1. Definition

• 랜덤 변수 : sample space S의 원소를 실수평면에 연결할 수 있도록 하는 함수
  • ex. 동전 던지기 - head를 1로, tail을 2로 정의한다.
  • P(X = a) = P( {s | X(s) = a} )
• 랜덤변수의 조건
  • x가 실수라면, $\{ s:X(s \leq x)\}$는 이벤트여야 한다.
  • 즉 $P(X\leq x) = P(\{s\in S : X(s)\leq x\})$
  • $P(X=-\infty) = P(X=\infty) = 0$ : R.V는 적정 범위 내에 있다.
• 이산/연속 랜덤변수
  • 이산 랜덤변수 : PMF(확률질량함수)
  • 연속 랜덤변수 : PDF(확률밀도함수)
• 랜덤 변수의 정의
  • Sample Space S = {1, 2, 3, 4} 가 있다고 생각한다.
  • 랜덤 변수 X는 X=X(s)=$s^3$으로 정의되어 있다.
  • S의 원소에 대한 확률을 다음과 같이 정의한다.
    • P({1}) = 4/24, P({2}) = 3/24, P({3}) = 7/24, P({4}) = 10/24
  • 이 때 랜덤변수 값의 확률은 다음과 같다.
    • P({X = 1}) = 4/24, P({X = 8}) = 3/24, P({X = 27}) = 7/24, P({X = 64}) = 10/24
    • X = $s^3$ = 8 이므로 s = 2, 즉 Sample space의 원소 {2}의 확률 3/24가 된다.

2. Distribution Function

• CDF(Cumulative probability Distribution Fuction) : 누적확률분포
  • $F_X(x) = P(X\leq x)$
  • $F_X(-\infty) = 0, F_X(\infty) = 1$
  • $F_X(x)$는 0과 1 사이, x는 실수
  • $F_X(x)$는 증가하는 함수이다
  • $P(x_1<X\leqq x_2) = F_X(x_2) - F_X(x_1)$
  • $F_X(x^+) = F_X(x)$ : right continuous
• Discrete R.V.에 대해
  • $F_X(x) = \sum_{i=1}^N P(x_i)u(x-x_i);$
  • $P(x_i) = P(X=x_i)$ : 확률질량함수(PMF)

3. Density Function

• PDF(probability Density Function) $f_X(x)$ : CDF의 미분형
• $f_X(x) = \frac{dF_X(x)}{dx}$
• 그냥 밀도함수라고도 부름
• PDF의 성질
  • $f_X(x)>0$일 때 x는 실수
  • $\int^\infty_{-\infty}f_X(x)dx = 1$
  • $F_X(x)=\int^x_{-\infty}f_X(x)dx$ : CDF는 PDF의 적분!
  • $P(x_1<X\leqq x_2) = \int^{x_2}_{x_1}f_X(x)dx$

4. Gaussian Distribution

• 노이즈 모델링 등에 사용 : 자연계 현상들은 미세 요소들의 중첩
• 정상 분포라고도 함(normal distribution)
• Gaussian PDF $f_X(x)=\frac{1}{\sqrt{2\pi\sigma^2}}exp(-\frac{(x-\mu)^2}{2\sigma^2})$
  $\mu$ : 평균, $\sigma^2$ : 분산 ( $\sigma$ : 표준편차 )
• CDF : $F_X(x)=\frac{1}{\sqrt{2\pi\sigma^2}}\int^x_{-\infty}f_X(t)dt$

  • special case : $a_X=0, \sigma_X=1$인 경우
    $F(x)=\frac{1}{\sqrt{2\pi}}\int^x_{-\infty}exp(-\xi^2/2)d\xi$

  • F(x)는 x에만 영향을 받는다

  • Normalization

    • $u=(\xi -a_X)/\Sigma_X$
    • $F_X(x) = F(\frac{x-a_X}{\sigma_X})$
    • ex. 평균 3, 표준편차 2를 갖는 가우시안 랜덤변수에 대해 event $\{X\leqq5.5\}$의 확률을 구하라.
      • $\frac{x-a_X}{\sigma_X}=\frac{5.5-3}{2}$ = 1.25
      • $P\{X\leqq5.5\} = F_X(5.5) = F(1.25) = 0.8944$

• Standard Cumulative normal table

5. Distribution

binomial distribution(이항분포)

• binomial density function
  • $f_X(x) = \sum^N_{k=0}\binom{N}{k}p^k(1-p)^{N-k}\delta(x-k)$
• binomial distribution function
  • $F_X(x) = \sum^N_{k=0}\binom{N}{k}p^k(1-p)^{N-k}u(x-k)$
• poisson distribution
  • 이산 랜덤변수에 대해 회수 N을 무한으로 늘렸을 때의 분포
  • 평균 확률을 $\lambda$, 구간을 T로 정의
  • $P(X=k) = \lim_{x\to\infty}\binom{N}{k}(\frac{\lambda T}{N})^k(1-\frac{\lambda T}{N})^{N-k}$

Uniform Distribution

• PDF $f_X(x)=\begin{cases} \frac{1}{b-a}\ (a\leq x\leq b)\\ 0\ (other) \end{cases}$
• CDF $F_X(x)=\begin{cases} 0\ (x<a)\\ \frac{x-a}{b-a}\ (a\leq x\leq b)\\ 1\ (x\geq b) \end{cases}$

Exponential Distribution

• PDF $f_X(x)=\begin{cases} \lambda e^{-\lambda x}\ (x \geq 0)\\ 0\ (X < 0) \end{cases}$
• CDF $F_X(x)=\begin{cases} 1-e^{-\lambda x}\ (x \geq 0)\\ 0\ (X < 0) \end{cases}$

Rayleigh Distribution

• x, y축 성분이 각각 가우시안 분포일 때 확률분포
• PDF $f_X(x)=\begin{cases} \frac{2}{b}(x-a)e^{-(x-a)^2/b}\ (x \geq a)\\ 0\ (X < a) \end{cases}$
• CDF $F_X(x)=\begin{cases} 1-e^{-(x-a)^2/b}\ (x \geq a)\\ 0\ (X < a) \end{cases}$

Conditional Distribution

• CDF $F_X(x|B) = \frac{P(\{X\leq x\}\cap B)}{P(B)} = P(X\leq x|B)$

  • Property
  1. $F_X(-\infty|B)=0$ (공집합)
  2. $F_X(\infty|B)=1$ (sample space)
  3. $x_1\leq x_2\ then\ F_X(x_1|B)\leq F_X(x_2|B)$
  4. $P({x_1<X\leq x_2}|B) = F_X(x_2|B)-F_X(x_1|B)$
  5. $F_X(x^+|B) = F_X(x|B)$

• PDF $f_x(X|B) = \frac{dF_X(x|B)}{dx}$

  • property
  1. $f_X(x|B) \geq 0$
  2. $\int^\infty_{-\infty}f_X(x|B)dx=1$
  3. $F_X(x|B)=\int^x_{-\infty}f_X(t|B)dt$
  4. $P({x_1<X\leq x_2}|B)=\int^{x_2}_{x_1}f_X(t|B)dt$

• Case 1. $B=\{X\leq b\}$

  • $F_X(x|B) = \frac{P({\{X\leq x\} }\cap \{X\leq b\})}{P(\{X\leq b\})}$

  • $F_X(x|B) = \begin{cases} \frac{F_X(x)}{F_X(b)}(x<b)\\ 1(x\geq b) \end{cases}$

  • $f_X(x|B) = \begin{cases} \frac{f_X(x)}{F_X(b)}(x<b)\\ 1(x\geq b) \end{cases}$

• Case 2. $B=\{X=a\}$

  • $F_X(x|B) = \begin{cases} 0(x<a)\\ 1(x\geq a) \end{cases}$

1. Set Definitions

• set(집합) : 원소의 모음
  • 유한 vs 무한 (셀 수 있는가 vs 없는가)
  • 셀 수 있는 무한집합 : 정수, 자연수, 유리수, 짝수, 홀수, ...
  • 셀 수 없는 무한집합 : 실수집합

2. Mathematical Model of Probability

• Sample space : 모든 가능한 결과의 집합

• Event : Sample space의 부분집합 (무한집합에서 효과적으로 사용)

• Probability : Event의 존재 확률

  • ex) 동전 던지기
  • Sample Space $U = \{앞, 뒤\}$
  • Event $A = \{\phi, \{앞\},\{뒤\},\{앞, 뒤\}$ ( $\{앞, 뒤\} : 앞면 or 뒷면$ )
  • Probability : $\phi = 0\ /\ {앞}={뒤}=\frac{1}{2}\ /\ {앞, 뒤} = 1$ (합집합 개념)

• Properties of probability

  1. sample space의 모든 event에서 $0\leq P(A)\leq 1$
  2. subset이 Sample Space와 동일할 때 $P(S)=1$
  3. $P(\cup^N_{n=1}A_n)=\sum^N_{n=1}P(A_n)$ (조건 : $A_m\cap A_n=\phi$)

• 확률(P)이 0이라도 이벤트(A)는 존재할 수 있다.

  • [0, 1] 범위의 실수 중 자연수 1을 뽑는다고 가정
  • 확률은 $1/\infty$이므로 0이지만, 1을 뽑는 사건은 존재

• 실제 실험에서의 수학적 모델

  1. sample space의 할당
  2. event의 정의
  3. 공리를 만족하도록 확률 할당
  • 현실에서의 확률 = 상대적 빈도
  • 실험을 통해 예측되는 확률과 진짜(real true) 확률의 구분이 필요

3. Joint and Conditional Probability

• Joint(교집합) : $P(A\cap B = P(A)+P(B)-P(A\cup B)$
• Conditional(조건부) : $P(A|B):=\frac{P(A\cap B)}{P(B)}$
  • A, B집합이 exclusive한 경우, $P(A|B)=0$

Bayes Theorem

• P(A) : 관찰된 것
• $P(B|A)$ : 사후 확률
• $P(A|B)$ : likelihood - 인과관계
• P(B) : 사전 확률 - 실험 전 일반적인 확률

• ex) binary communication system

• $P(B_1|A_1)$ : 결과값 $A_1$이 $B_1$에서 온 값일 확률
• $P(A_1)=P(A_1|B_1)P(B_1) + P(A_1|B_2)P(B_2)$
  $= 0.9\times0.6+0.1\times0.4=0.58$
  $\therefore P(B_1|A_1)=P(A_1|B_1)P(B_1)/P(A_1)=0.9\times0.6/0.58\simeq0.931$

4. Independent Events

• 두 사건이 통계적으로 독립적이라는 것은
• $P(A|B) = P(A),\ P(B|A) = P(B)$이고 $P(A\cup B)=P(A)P(B)$ 이다.
• 또한 두 사건의 교집합은 공집합이 아니어야 한다.
• Multiple Events
  • N개의 사건이 있을 때 독립이기 위해 아래 조건을 충족해야 한다.

5. Combined Experiment

• 2개의 sample space가 중첩된 경우
• $S = S_1 \times S_2$
• 즉 sample space $S = \{s_1, s_2)|s_1\in A\ and\ s_2\in B\}$
• $P(A\times B) = P(A)P(B)$

• Permutation
  • 순열 $_nP_r=\frac{n!}{(n-r)!}$
  • 중복순열 $_n\Pi_r=n^r$
• Combination
  • 조합 $_nC_r=\binom{n}{r}=\frac{_nP_r}{_rP_r}=\frac{n!}{(n-r)!r!}$
  • 중복조합 $_nH_r =\binom{n+r-1}{n-1}=\binom{n+r-1}{r}$

Bernoulli Trials

• 2개의 사건 $A : P(A)=p,\ \overline{A} : P(\overline{A})=1-p$일 때
• N번의 실행을 한다면

  • 1회차의 발생 확률 : $p^k(1-p)^{N-k}$

  • A가 k번 나타나는 시도 : $\binom{N}{k}$

  • P(A가 k번 나타날 확률) = $\binom{N}{k}p^k(1-p)^{N-k}$

• 많은 회수 N번 시도하였을 때의 확률 : De Moivre-Laplace approximation

  • $\binom{N}{k}p^k(1-p)^{N-k}\approx\frac{1}{\sqrt{2\pi Np(1-p)}}exp(-\frac{(k-Np)^2}{2Np(1-p)})$

  • $\mu$ : 평균, $\sigma^2$ : 분산일 때 가우시안 분포 $\frac{1}{\sigma\sqrt{2\pi}}exp(-\frac{(x-\mu)^2}{2\sigma^2})$

  • 다회 반복에 대해서 베르누이 분포 확률은 가우시안 분포와 유사한 값을 띈다

  • 확률 $\mu = Np$, 분산 $\sigma^2 = Np(1-p)$

• Poisson approx. : De Moivre-Laplace Approx. 에서 충분히 작은 p값에 대해
  • $\binom{N}{k}p^k(1-p)^{N-k}\approx\frac{(Np)^{k_e-N_p}}{k!}$