[자동제어] 6. The Frequency Response Design Method

6. The Frequency Response Design Method

1. Frequency Response

• 주파수 응답 : 선형시스템에 sinusoidal 입력이 들어갔을 때의 응답
  • 입력 $u(t)=Asin(w_0t)$
  • 초기값 0일 때 출력 $Y(s)=G(s)\frac{Aw_0}{s^2+w_0^2}$
  • G(s)가 n개의 pole을 갖는다고 할 때,
    $Y(s)=\frac{\alpha_1}{s-p_1}+\frac{\alpha_2}{s-p_2}+...+\frac{\alpha_n}{s-p_n}+\frac{\alpha_0}{s+jw_0}+\frac{\alpha_0^*}{s-jw_0}$
  • $\alpha_0=\lim_{s\rarr -jw_0}G(s)\frac{Aw_0}{s^2+w_0^2}=-\frac{A}{2j}G(-jw_0)$
  • $\alpha_0^*=\frac{A}{2j}G(jw_0)$
• 주파수 응답 $y(t)$
  $=\alpha_1e^{-p_1t}+\alpha_2e^{-p_2t}+...+\alpha_ne^{-p_nt}+\frac{A}{2j}[G(jw)e^{jw_0t}-G(-jw)e^{-jw_0t}]$
  $=\alpha_1e^{-p_1t}+\alpha_2e^{-p_2t}+...+\alpha_ne^{-p_nt}+|G(jw_0)|Asin(w_0t+\phi)$
  • $\phi=tan^{-1}\frac{Im[G(jw_0)]}{Re[G(jw_0)]}$
  • 안정적인 시스템 응답이 steady state가 되는 경우, pole 항은 모두 소거 :
    $y(t)=|G(jw_0)|Asin(w_0t+\phi)=AMsin(w_0t+\phi)$
  • 주파수 응답 특성(Frequency Response Characteristics) : 시스템의 sinusoidal 입력에 따른 고유한 Magnitude, Phase의 주파수 응답 특성

---

• Bode Plot : 사인파 입력의 주파수가 변화함에 따라 응답의 Magnitude, Phase 변화를 각각 나타내는 그래프

  • x축(주파수) : log scale
  • y축(Magnitude) : log scale
  • y축(phase) : linear scale
  • Compensator 설계에 활용 가능
  • 각 시스템의 bode plot은 더해질 수 있다.
  • log scale이므로 광범위한 응답특성 표현 가능

• System $G(jw)=\frac{\vec{s_1}\vec{s_2}}{\vec{s_3}\vec{s_4}\vec{s_5}}$일 때

  • $\vec{s}=re^{j\theta}$
  • $M=|G(jw)|,\ \phi=\angle G(jw)$
  • $logM=log\sum r,log\angle G(jw)=j(\sum\phi)loge$
  • $|G|_{db}=10log\frac{P_2}{P_1}=20log\frac{V_2}{V_1}$

• Bode Form : 시스템 인수의 상수값이 1

  • $KG(s)=K\frac{(s-z_1)(s-z_2)...}{(s-p_1)(s-p_2)..}$
    $\rarr KG(jw)=K_o\frac{(jw\tau_1+1)(jw\tau-2)...}{(jw\tau_a+1)(jw\tau_b+1)...}$

---

• 전달함수 형태
  • $K_0(jw)^n$
  • $(jw\tau+1)^{\pm1}$
  • $[(\frac{jw}{w_n})^2+2\zeta(\frac{jw}{w_n})+1]^{\pm1}$

---

• ex. Class-1 : $K_0(jw)^n$

  • (dB) $M=20log|K_0(jw)^n|=20log|K_0|+20nlogw$
  • $\angle(jw)^n=n\times90\degree$
  • Magnitude : $K_0=1,\ n=1$이라고 하면, 20dB/decade의 기울기를 갖는 직선 그래프 생성
    

    

  • Phase : $n\times90\degree$의 x축과 평행한 직선 그래프

• ex. Class-2, 1st-order : $jw\tau+1$

  • Magnitude
    

    

    • $w\tau<<1\rarr log|jw\tau+1|\simeq0$
    • $w\tau+1>>1\rarr log|jw\tau+1|\simeq log|\tau|+log|jw|$
    • $w\tau=1$ : Break Point
      • $M=20log|j+1|=20log\sqrt{2}\simeq3dB$
    • $((w=1/\tau),0dB)$ 좌표를 기준으로 0dB/dec, 20dB/dec 기울기의 점근선 형성
    • $(jw\tau+1)^{-1}$ 의 경우 -3dB 점을 기준으로 -20dB/dec 기울기로 감소하는 그래프 형성
  • Phase
    

    

    • $w\tau<<1\rarr 0\degree$
    • $w\tau+1>>1\rarr 90\degree$
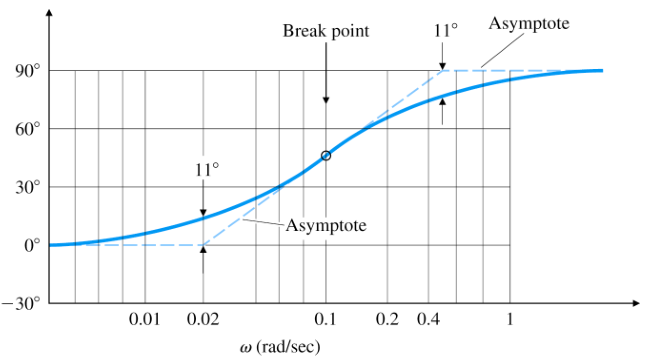
    • Break Point : $w\tau=1\rarr 45\degree$
    • 점근선의 기울기, $90\degree,\ 0\degree$의 점근선을 기준으로 하는 곡선 그래프 형성

• ex. Class-3, 2nd-order term : $[(\frac{jw}{w_n})^2+2\zeta(\frac{jw}{w_n})+1]^{\pm1}$

  • Magnitude
    

    

    • $w<<w_n\rarr log|G(jw)|\simeq0$
    • $w>>w_n\rarr G(jw)\simeq(jw/w_n)^{\pm2}$
      $log|G(jw)|\simeq\pm2log|1/w_n|\pm2log|jw|$
    • $w=w_n\rarr log|G(jw)|\simeq log((2\zeta)^{\pm1})$
    • breakpoint에서 $20log(2\zeta)^{\pm1}$ 지점을 통과
  • Phase
    

    

    • 차단주파수 전후로 0, 180도의 위상, breakpoint에서 $\angle G(jw)=-\angle j2\zeta$
    • $zeta$가 1에 가까울 수록 완만하게, 0에 가까울수록 급격하게 그래프 변화

---

• Bandwidth : Closed-Loop Transfer function
  • Amplitude가 1 > 0.707로 감소할 때의 주파수
  • 이 때 Magnitude는 약 -3dB
  • 전력이 50% 이하로 감소

---

• Bode Plot 작성
  1. Magnitude : 전달함수를 Bode Form으로 조절 : $KG(jw)=K_o\frac{(jw\tau_1+1)(jw\tau-2)...}{(jw\tau_a+1)(jw\tau_b+1)...}$
  2. 주파수를 0으로 근사시켜 기울기 확인 후, 주파수 w=1일 때 점근선 작성
  3. 각 breakpoint에서의 점근선 작성 : 먼저 작성한 점근선 그래프에 breakpoint 주파수를 대입하여 그 지점을 지나는 점근선으로 작성
  4. 기울기가 감소, 혹은 증가할 때 Bode Plot 곡선은 교차점에서 $\pm3dB$ 차이나는 지점을 지나게 된다.
  5. Phase : 주파수를 0으로 근사시켜 출발점 위상 확인
  6. zero를 지나면 +90, pole을 지나면 -90도씩 변화하는 점근선 작성
  7. Phase Bode Plot 작성 : 곡선은 변화하는 점근선의 중간점을 지남

---

2. Neutral Stability

• $KG(s)$의 전달함수에서 얻은 Bode Plot으로 Closed-Loop system의 안정도 판별
  • Closed-Loop system의 root locus 작성시
    모든 점에서 $1+KG(s)=0\rarr |KG(s)|=1$, $\angle G(s)=180\degree$
  • 허수축 위를 지날 때 (neutral stability) : $|KG(jw)|=1$, $\angle G(jw)=180\degree$

---

• $G(s)=\frac{1}{s(s+1)^2}$에서 $\angle G(jw)=-180\degree$일 때,
  • K=2이면 $|KG(jw)|=1$
  • K<2이면 $|KG(jw)|<1$ : Stable
  • K>2이면 $|KG(jw)|>1$ : Unstable
  • 즉 $\angle G(jw)=-180\degree$일 때 $|KG(jw)|<1$ 이면 Stable
• 만약 $G(s)=s(s+1)^2$이면 $\angle G(jw)=-180\degree$일 때 $|KG(jw)|>1$ 이면 Stable

---

• Bode Plot의 경우 Gain이 1 (위상이 180도)인 지점을 여러번 지날 수 있어 안정도 판별에 어려움 존재
• Nyquist 안정도 판별법을 대신 사용

---

3. Nyquist Stability

• 편각의 원리
  

  

  • 전달함수 H(s)에서 s가 임의의 궤적 C1을 따를 때,
  • H(s)의 궤적은 s의 궤적 C1 안에 속하는 Zero - Pole 개수 차이만큼 원점을 포함하여 회전하는 궤적이 된다.
  • zero가 더 많으면 시계방향, pole이 더 많으면 반시계방향
• $C_1$궤적을 RHP 모두를 포함하는 궤적으로 가정
  

  

  • RHP에 zero 존재 : 시계방향 궤적
  • RHP에 pole 존재 : 반시계방향 궤적
• 전달함수 $T(s)=1+KG(s)=1+K\frac{b(s)}{a(s)}=\frac{a(s)+Kb(s)}{a(s)}$일 때
  • G(s)의 RHP Pole = 1+KG(s)의 RHP pole
  • closed-loop의 RHP Pole = 1+KG(s)의 RHP zero
  • N = Z-P
    • N : 원점을 포함하며 시계방향으로 회전하는 궤적 수
    • Z, P : T(s)의 RHP zero, pole 개수
    • Z = N+P이므로, T(s)의 RHP zero가 없다면 G(s)의 RHP pole이 없으므로 안정된 시스템이다.

---

• Nyquist Plot의 작성법
  1. RHP 궤적 $C_1$을 3개 영역에 나누어 KG(s)분석
     • $0\rarr j\infty$
     • $-j\infty\rarr0$
     • RHP를 따라 이동하는 Big Arc
       • 무한의 반지름을 따라 이동하므로 $KG(j\infty)$계산
       • $KG(j\infty)$ 는 pole 차수가 더 클때 0, pole, zero 차수가 동일하면 상수
  2. KG(s)의 Bode Plot 작성
     • breakout point의 좌표 확인
  3. Bode Plot을 기반으로 Nyquist Plot 작성
     • Bode Plot에서 위상 0도일 때의 Gain = + 방향 X축에서의 시작 좌표
     • 위상 변화에 따라 Gain 크기가 궤적의 반지름
  4. 궤적의 Loop 내에 포함되는 원점의 개수 확인

---

• ex. $G(s)=\frac{1}{s(s+1)^2}$
• s가 매우 작은 값이 될 때, $G(s)\simeq \frac{1}{s}$로 근사
  • r이 0으로 근사 시 매우 큰 값이 된다
  • r이 무한으로 증가하면 궤적은 원점 근처를 지난다
  • 위상 $\phi$는 -90~ 90도로 이동하는 궤적이므로 G는 반시계방향 (90 ~ -90도)으로 이동하는 궤적이 된다.
  • Bode plot 작성 시 w값이 -90에 가까울 수록 Gain이 커지고, -180도에서 0, 이후로 급격히 작아지므로 3사분면에서 시작하여 w=1 지점을 끼고 원점으로 수렴하는 궤적이 나타난다.