[반도체공학] 4.3. Diffusion

3. Diffusion

1. Diffusion

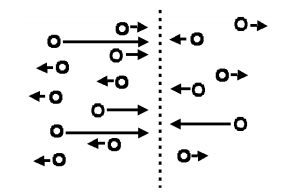
• 입자 농도(화학적 포텐셜)의 기울기(Gradient)$\\$ + 열에너지, Scattering에 의한 Random Motion에 의해 발생
  • Random Motion : 고농도 / 저농도측 모두 입자가 랜덤한 양으로 이동$\\$경계를 통과하는 입자수는 고농도측 입자가 더 많음$\\$결과적으로 시간이 지나면 두 영역이 평형 상태가 됨
• 높은 농도에서 낮은 농도로 입자가 이동(재분배)
• 평형 상태가 될 때까지 이동
  • 반도체의 경우 Charged Particle에 의해 Diffusion이 끝나도 같은 농도가 아닐 수 있음

---

2. Diffusion Current

• Diffusion에 의한 입자 흐름
  • $\mathcal{F}=-D\nabla\eta$
  • diffusion flux = -(diffusion Coefficient)×Grad(Concentration)
  • $\nabla\eta$가 ( - ) : diffusion은 농도가 감소하는 쪽으로 발생
• 전자 diffusion current density : $J_{Ndiff}=qD_N\nabla n$
  • 전자 diffusion은 농도가 낮은 쪽으로 이동
  • 전자와 전류의 방향은 반대이므로 $J_{Ndiff}$는 ( + )
• 정공 diffusion current density : $J_{Pdiff}=-qD_P\nabla p$
  • hole diffusion은 농도가 낮은 쪽으로 이동
  • hole diffusion과 current 같은 방향이므로 $J_{Pdiff}$는 ( - )

---

• Total Current = Drift + Diffusion
  • hole : $J_P=J_{Pdrift}+J_{Pdiff}=qp\mu_pE-qD_P\nabla p$
  • electron : $J_N=J_{Ndrift}+J_{Ndiff}=qn\mu_nE+qD_N\nabla n$
  • $J=J_P+J_N$
• Drift Current는 전기적 포텐셜에 영향을 많이 받아 Majority Carrier의 영향을 크게 받지만$\\$Diffusion Current는 농도차의 영향을 받으므로 Major 뿐 아니라 Minority Carrier의 영향 역시 유의미하게 존재한다.

---

• Built-in Electric Field
  • 캐리어 농도가 불균일한 상태로 평형 상태가 되도록 하는 힘
  • $J_N=J_P=0$일 때 equilitbrium
  • equilibrium일 때 전류밀도의 식을 이용하면
    • electric field $E=\frac{D_p\nabla p}{\mu_pp}=-\frac{D_n\nabla n}{\mu_nn}$
    • equilibrium 상태여도 농도차의 항 $\nabla n,\ \nabla p$는 존재
    • uniform doping 인 경우 $\nabla n=\nabla p=0$, electric field=0
    • 불균일한 doping인 경우 $\nabla n,\ \nabla p\not =0\\$평형 상태에서 $J=0$이 되기 위해 built-in electric field가 존재하게 됨.

---

• Hot Point Probe Measurement

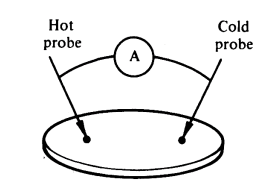
• 온도가 높은 probe와 낮은 probe 사이에 전류계를 연결
• hot probe 쪽의 입자가 더 활발하게 움직이는 점을 이용한 전류 측정
• p-type 입자가 더 많은 경우 전류가 ( - ), n-type입자가 더 많은 경우 ( + )

---

3. Energy Band Diagram

• 가로축 : x 방향
• 원점의 valance band를 $E_{ref}$로 가정
• reference energy를 기준으로
  • electron potential energy : $E_C(x)-E_{ref}$
  • hole potential energy : $E_{ref}-E_V(x)$
  • conduction band 초과치 : electron kinetic energy
  • valance band 초과치 : hole kinetic energy
  • total energy = kinetic + potential

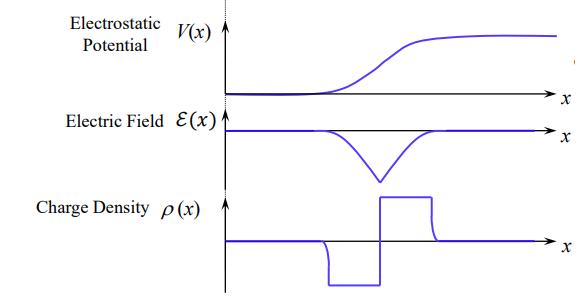
• Electic potential $V_(x)=-\frac{1}{q}[E_C(x)-E_{ref}]$
  • $E_C$ 대신 $E_i,\ E_V$값이 들어갈 수 있음
  • heavy doping이 아닌 이상 $E_C,\ E_i,\ E_V$는 parallel
  • 이전 그림에서 $E_c(x)$는 x에 비례하여 감소하므로 전위는 증가
• Electric Field $E(x)=-\nabla V(x)=\frac{1}{q}\nabla E_C(x)$
  • 전위가 중간에 증가하고 양 끝단에서는 일정 값을 유지하므로 중간 지점에서 강하게 나타남
• Charge Density $\rho(x)=\nabla\cdot D(x)=\nabla\cdot[\epsilon E(x)]=-\epsilon\nabla^2V(x)$

---

• Equilibrium
  • 모든 순/역방향 캐리어 이동이 동등한 상태
  • 물리적 관측량은 변화가 없음
  • 일정한 fermi level : $\nabla E_F,dE_F(x)/dx=0$
  • Net current가 0 : $J_P+J_N=0$
  • Net carrier generation/recombination이 0 :$\\$ nondegenerate 반도체에서 $np=n_i^2$
  • 불균일 도핑의 경우 diffusion에 의한 전류를 drift 전류가 상쇄한다(built-in electric field)

---

4. Band Bending

• 불균일한 도핑이나 applied electric field는 nonzero electric field, chage imbalance를 유발
• nonzero electric field : potential 에너지의 기울기 존재, band banding 발생
  • electron/hole drift 전류가 존재
  • drift 전류 상쇄를 위한 diffusion current 존재
  • the law of detailed balance : equilibrium 상태에서$\\$ 총 electron/hole 전류는 0, 페르미 준위는 constant ($np=n_i^2$)
• equilibrium = 페르미 준위가 상수이고, 하나의 값을 갖는 상태
  • 상수 페르미 준위 = 전자/정공 전류는 0
  • 단일 페르미 준위 = 캐리어 생성/결합 비율이 동일

---

• non-uniformly doped semiconductor

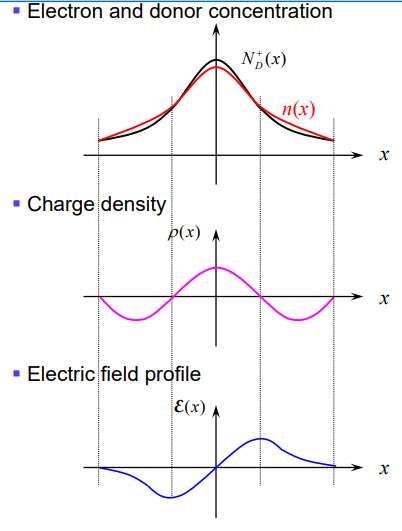
• 이온화된 donor는 (+), 전자(n)은 (-) charge
  • 가운데는 donor가 더 많아 전하밀도가 (+), 양 끝은 전자가 많아 (-)
  • 전하밀도 $\rho$는 전계의 기울기이므로 기함수 형태의 전계 그래프가 형성

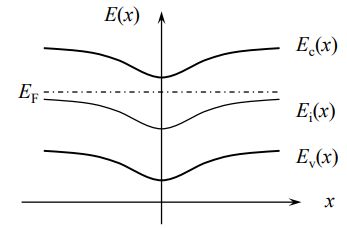
• $E_F$는 상수이고, 양 끝단에서는 $E_F-E_i$가 작고 중앙에서는 커지는 모양을 형성하여야 함
• $np=n_i^2$의 식을 만족하기 위해 $E_c, E_i$도 같은 모양을 형성

---

5. Einstein Relationship

• Constancy of Fermi level in Equilibrium
  • 임의 지점 1, 2에서의 fermi level을 $E_{F1},\ E_{F2}$로 가정
  • 이 지점에서의 온도를 $T_1, T_2$로 가정
  • 입자의 이동 비율 $r_{12}=R_0f(E_1)[1-f(E_2)]$, $r_{21}=R_0f(E_2)[1-f(E_1)]$
    • equilibrium일 때 $r_{12}=r_{21},\ f(E_1)=f(E_2)$
  • 모든 E에 대해 $E_{F1}=E_{F2},\ T_1=T_2$
  • 즉, $\nabla E_F=0$
• Detailed Balance
  • equilibrium 상태에서 $J_N=J_P=0,\ J=J_N+J_P=0$

---

• Einsetin Relationship

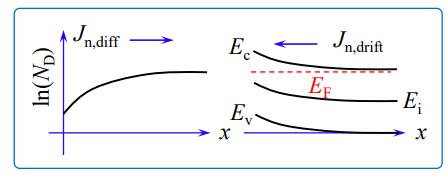
• diffusion current는 donor 농도가 높아지는 쪽으로 이동
• drift current는 Energy Band level이 높아지는 쪽으로 이동
• equilibrium 상태에서 $J_{Ndrift}+J_{Ndiff}=qn\mu_nE+qD_N\frac{dn}{dx}=0$
  • $E=\frac{1}{q}\nabla E_i(x)$ (electric field = intrinsic band level의 미분값)
  • $n=n_iexp[(E_F-E_i)/kT]$
  • $dn/dx=-\frac{n}{kT}[\frac{dE_F}{dx}-\frac{dE_ i}{dx}]$
  • $dE_F/dx=0$이므로 $dn/dx=-\frac{q}{kT}nE$
  • $\therefore J_N=qnE(\mu_n-\frac{qD_N}{kT})$
• 전자의 einstein relationship : $\frac{D_N}{mu_n}=\frac{kT}{q}$
• 정공의 einstein relationship : $\frac{D_P}{\mu_p}=\frac{kT}{q}$
• einsteint relationship : 물질 간의 관계 - equilibrium 여부와는 무관
• diffusion coefficient(by diffusion)와 mobility(by drift) 둘 다 scattering에 영향을 받기 때문에, 비례관계를 갖게 된다.