728x90
2. Dynamic Models

2. Dynamic Models

  • 컨트롤러 설계 전에 구하는 시스템 제어를 위한 시스템의 수학적 표현식
  • 시스템의 동작을 나타내는 미분방정식
  • 기계적 시스템, 전기회로, 전기적(electromechanical) 시스템

2.1. Dynamics of Mechanical Systems

  • 뉴턴의 법칙 - translational motion F⃗=ma⃗\vec{F}=m\vec{a}
  • F⃗\vec{F} : 질량에 가해지는 힘의 벡터합
  • a⃗\vec{a} : 질량에 가해지는 관성 가속도
  • mm : 질량
  • 1N=1kg⋅m/sec21N = 1kg\cdot m/sec^2
  • ex 1. Cruise-control model
    • 자동차는 수평 방향으로 이동한다고 가정
    • 바퀴의 회전관성은 무시
    • 자동차-지면 사이의 마찰력은 속도에 비례
    • u−bx‘=mx‘‘u-bx`=mx``
    • (구하려는 값은 속도x‘≔vx`\coloneqq v)v‘+bmv=umv`+\frac{b}{m}v=\frac{u}{m}
    • (라플라스 변환)sV(s)+bmV(s)=U(s)msV(s)+\frac{b}{m}V(s)=\frac{U(s)}{m}
    • V(s)U(S)=1/ms+b/m\frac{V(s)}{U(S)}=\frac{1/m}{s+b/m}
  • ex 2. suspension system
    • 서스펜션은 오직 1차원 수직운동을 한다.
    • 자동차 바퀴에는 무게가 균등하게 분산된다.
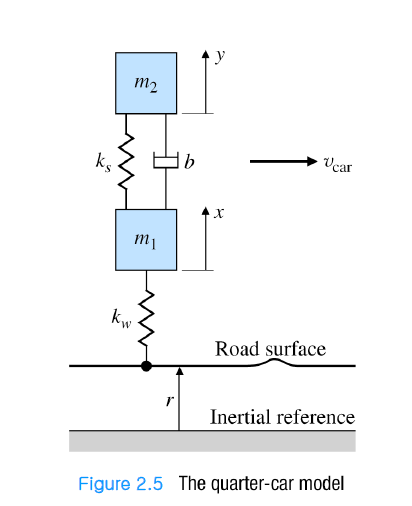
    • m1m_1 : 타이어의 무게 / m2m_2 : 자동차 무게의 1/4
    • x : 타이어의 변위 / y : 차체의 변위 / r : 높이의 변화
    • k : 용수철의 탄성계수 / b : 댐퍼 계수
    • 변위에 따른 응답을 계산하므로 중력가속도에 의한 힘 m1g, m2gm_1g,\ m_2g는 상쇄되어 사라진다.
    • 정해진 상황(ex. m2는 멈춘 채로 m1만 위로 움직인다)에 대한 differential eq.를 구하더라도 그 식은 시스템 내의 고유한 응답을 나타내는 식이기 때문에 다른 상황에 대해서도 성립할 수 있게 된다.
    1. m1m_1만 움직이는 경우
      • 아래 스프링 kwk_w는 늘어나고, 위 스프링 ksk_s는 압축된다.
      • 지변 변위를 고려하면 아래로 가해지는 힘은 kw(x−r)k_w(x-r)
      • 위 스프링의 경우 m2m_2가 y방향으로 이동할 것을 고려하면 스프링의 힘은 ks(y−x)k_s(y-x) (x, y 둘다 지면 변위의 영향을 받으므로 식에서는 상쇄된다.)
      • 댐퍼 역시 y방향 변위를 고려하면 b(y′−x′)b(y'-x')
    2. m2m_2만 움직이는 경우
      • 스프링에 의한 힘 ks(y−x)k_s(y-x)
      • 댐퍼에 의한 힘 b(y‘−x‘)b(y`-x`)
    3. 입력 : 높이 변위 r / 출력 : 자동차의 높이 변화 y
      • i. b(y′−x′)+ks(y−x)−kw(y−x)=m1x‘‘b(y'-x')+k_s(y-x)-k_w(y-x)=m_1x``
      • ii. −[b(y‘−x‘)+ks(y−x)]=m2y‘‘-[b(y`-x`)+k_s(y-x)]=m_2y``
      • ii를 x에 대해 정리 후 i에 대입하면 Y(s)R(s)=kw(sb+ks)/m1m2s4+b(1m1+1m2)s3+(ksm1+kwm1+ksm2)s2+kwbm1m2s+kwksm1m2\LARGE{\frac{Y(s)}{R(s)}=\frac{k_w(sb+k_s)/m_1m_2}{s^4+b(\frac{1}{m_1}+\frac{1}{m_2})s^3+(\frac{k_s}{m_1}+\frac{k_w}{m_1}+\frac{k_s}{m_2})s^2+\frac{k_wb}{m_1m_2}s+\frac{k_wk_s}{m_1m_2}}}
  • 회전운동에 대한 뉴턴운동의 법칙
    • M=IαM=I\alpha
    • M : 회전 중심에 대한 모멘트의 합
    • I : 무게중심에 대한 회전관성모멘트 (I=ml2I=ml^2)
    • α\alpha : 각가속도
    • ex. Pendulum
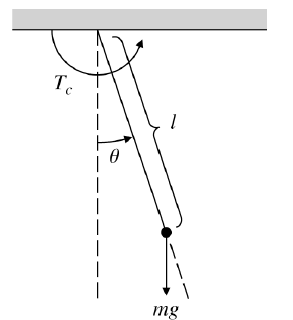
    • 운동방정식 TC−mglsinθ=Iθ′′T_C-mglsin\theta=I\theta''
    • θ′′+glsinθ=TCml2\theta''+\frac{g}{l}sin\theta=\frac{T_C}{ml^2}
    • 작은 운동에 대해서 sinθ≃θsin\theta\simeq\theta
    • Transfer Eq. Θ(s)TC(s)=1/ml2s2+g/l\frac{\Theta(s)}{T_C(s)}=\frac{1/ml^2}{s^2+g/l}
  • 실험 오차
    • 펜듈럼 모델을 Matlab으로 실험하여 보면 정현파 형태로 나타나는 것을 확인 가능하다.
    • 계산 편의상 단순화한 부분들에 대해 오차가 발생하기 때문에 실제 실험 결과와는 차이가 발생할 수밖에 없다.
  • ex. 회전 운동과 직선 운동의 조합
    • 질량 mt,mpm_t, m_p인 크레인과 펜듈럼이 각각 직선/회전운동
    • 힘 μ\mu가 가해지며, 차량은 x방향으로 이동
    1. 회전운동
    • 중력에 의해 지면 방향으로의 회전운동이 발생 : −mpglsinθ-m_pglsin\theta
    • 크레인의 직선운동에 의한 펜듈럼의 관성 : mpx′′cosθm_px''cos\theta
    • ∴(I+mpl2)θ′′=−(mpx′′cosθ+mpglsinθ)\therefore (I+m_pl^2)\theta''=-(m_px''cos\theta + m_pglsin\theta)
    1. 직선운동
      • 작용-반작용 N과 마찰계수 b를 고려
      • u−N−bx′=mtx′′u-N-bx'=m_tx''
      • 펜듈럼에 의한 반작용
        • 펜듈럼 운동 mpx′′m_px''
        • 회전 운동 mplθ′′cosθm_pl\theta''cos\theta
        • 구심력 mv2r=mpl(θ′)2sinθ\frac{mv^2}{r}=m_pl(\theta')^2sin\theta
        • N=mpx′′+mplθ′′cosθ−mpl(θ′)2sinθN=m_px''+m_pl\theta''cos\theta-m_pl(\theta')^2sin\theta
    • simplify : b=0,θ≃0⇒sinθ=θ,cosθ=1b = 0, \theta\simeq0 \rArr sin\theta = \theta, cos\theta = 1
      • 회전운동 : −mplx′′−mpglθ=(I+mpl2)θ′′-m_plx''-m_pgl\theta=(I+m_pl^2)\theta''
      • 직선운동 : (mt+mp)x′′+mplθ′′=u(m_t+m_p)x''+m_pl\theta''=u
    • 라플라스 변환
      • 회전운동 : −s2mplX(s)−mpglΘ(s)=s2(I+mpl2)Θ(s)-s^2m_plX(s)-m_pgl\Theta(s)=s^2(I+m_pl^2)\Theta(s)
      • 직선운동 : s2(mt+mp)X(s)+s2mplΘ(s)=U(s)s^2(m_t+m_p)X(s)+s ^2m_pl\Theta(s)=U(s)
    • 회전운동의 식을 X(s)X(s)에 대해 정리 후 직선운동에 대입하면
    • Θ(s)U(s)=−mpl((l+mpl2)(mt+mp)−mp2l2))s2+mpgl(mt+mp)\frac{\Theta(s)}{U(s)}=\frac{-m_pl}{ ((l+m_pl^2)(m_t+m_p)-m_p^2l^2))s^2+m_pgl(m_t+m_p)}
    • 전달함수의 단점 : 단일 입력-단일 출력(SISO)에 대한 수식 모델 설계 가능
  • 정리
    1. 대상 시스템의 dynamic behavior 단순화
    2. free-body diagram
    3. 뉴턴의 법칙 / 회전운동 / 전자회로 등을 이용한 미분방정식
    4. 초기값 = 0인 조건 하에 Laplace Transform
    5. Transfer function = 출력 / 입력
728x90
저작자표시 비영리 변경금지

+ Recent posts

티스토리툴바