전자공학[마감]/반도체공학
[반도체공학] 5.2. PN Junction Electrostatics
jehunseo
2020. 6. 9. 10:02
2. pn junction Electrostatics
2. pn junction Electrostatics
1. General Introduction: Poisson’s Equation
- pn junction : special case of non-uniform doping

- P/N 영역에서는 각각 균일하게 도핑되어있지만, 접합된 전체 반도체는 불균일한 상태
- Non-uniform doping : Carrier Diffusion, space charge, built-in electric field(potential), band-bending
- Poisson's Equation : space charge와 내부 전계(전위) 사이의 관계식
- ∇⋅E=ϵ0KSρ(x,y,z)=−∇2V(x,y,z)
- 1차원 푸아송 방정식
- dxdE(x)=−dx2d2V(x)=ϵ0ϵrρ(x)
- ρ(x)=q[p(x)−n(x)+ND(x)−NA(x)] (full-ionization 가정)
- V=−Ei/q이므로
qϵ0ϵrdx2d2Ei(x)=q[niexp[(Ei(x)−EF)/kT]−niexp[(EF−Ei(x))/kT]+ND(x)−NA(x)]
- uniform doping을 가정해도 식이 매우 nonlinear하므로 해를 구하기가 어려움
- Band Bending

- N/P 도핑은 각각 uniform하지만, 불균일에 의해 비선형으로 분포
2. Major Features Conjecturable
- Metallurgical junction에서 멀리 떨어진 영역은 원래의 uniform doping 상태를 유지한다.
- 페르미 준위는 상수이다 (g=r, JN=JP=0)
- Metallurgical junction 근처에서 band bending과 space charge를 관찰할 수 있다.
- space charge의 크기 :
{q(p−n−NA)≃−qNA (@p−region)q(p−n+ND)≃qND (@n−region)
- 접합 근처에서 p≃n≃ni<<NA(ND)
- JP=JN=0
- p, n에 의한 built-in electric field의 크기는 같고, 캐리어 양에 비례한다.
- E(x)=qkTp(x)1dxdp(x)=−qkTn(x)1dxdn(x)
- 전하량 보존 법칙 : p-region과 n-region에 형성된 전하량의 총량은 동일
3. Equilibrium Energy Band Diagram
- p/n-type 반도체는 각각 uniform하게 도핑된 상태로 접합

- Metallurgical junction에서 멀리 떨어진 영역은 원래의 uniform doping 상태를 유지한다.

- 두 반도체가 접합했을 때, 페르미 준위는 일정

- 이 조건을 만족하기 위해서 접합 시 p-type 반도체의 준위는 n-type 대비 높아지게 됨 ( n-type반도체의 준위가 p-type 대비 낮아지게 됨 )
- 접합 후 energy band는 연속적으로 변화하는 형태로 나타남

4. Built-in Potential
- built-in potential : n/p-type의 EC(EV,Ei)차이만큼 나타남
- [EF−Ei]n=kTln(ninn0)≃kTln(niND)
- [Ei−EF]p=kTln(nipp0)≃kTln(niNA)
- built-in potential qVBI=kTln(ninn0)+kTln(nipp0)
≃kTln(niND)+kTln(niNA)≃kTln(ni2NAND)
- Built-in electric field : E(x)=−dxdV(x)
-
VBI=−∫−xcpxcnE(x)dx=∫xcn−xcpdV=V(xcn)−V(−xcp)
( xcn, xcp : Bulk region )
-
equilibrium : JN=qn(x)μn(x)E(x)+qDN(x)dxdn(x)=0
E(x)=−μn(x)DN(x)n(x)1dxdn(x)=−qkTn(x)1dxdn(x)
-
VBI=−∫−xcpxcnE(x)dx=∫−xcpxcnqkTn1dxdndx
=qkT∫−xcpxcnn1dn=qkTln[n(−xcp)n(xcn)]
-
n(xcn)≃ND, n(−xcp)≃NAni2이므로
qVBI=kTln[ni2nn0pp0]≃kTln[ni2NDNA]

- Metallurgical junction (ND−NA=0)과 Intrinsic point (EF−Ei=0)은 p/n-type 반도체의 도핑 농도에 따라 달라질 수도 있다.
5. Electrostatic Consideration

- non-uniform doping
→ concentration(potential) gradient
→ built-in electric field
→ drift/diffusion current, Charge Density
- V(x)∝−Ec(x)/q,−Evx)/q,−Ei(x)/q
- E(x)=−dxdV(x)=q1dxdEi(x)
- ρ(x)=dxdD(x)=ϵ0ϵsdxdE(x)=−ϵ0ϵsdx2d2V(x)
=q[p(x)−n(x)+ND(x)−NA(x)]
- p(x)=niexp[(Ei(x)−EF)/kT]
- n(x)=niexp[(EF−Ei(x))/kT]
- space charge
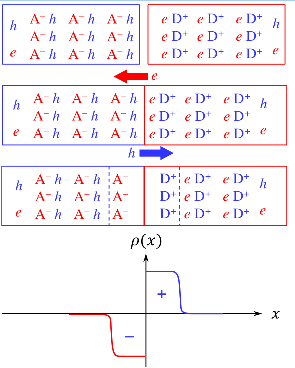
- n-type 반도체는 D+, e 캐리어를, p-type 반도체는 A−, h 캐리어를 보유
- 두 반도체가 접하게 되면 전자와 정공은 서로 결합하여 사라짐
- 남은 D+, A−가 depletion region의 space charge, built-in electric field 형성
- 내부 전계의 drift current에 의해 전자, 정공의 diffusion current 상쇄
6. Depletion Approximation
- 해를 구하기 위한 단순화
- Grown step junction + space charge는 불연속적으로 변화함을 가정
- ρ(x)≃⎩⎪⎪⎪⎪⎨⎪⎪⎪⎪⎧0:x<−xp−qNA:−xp≤x<0qND:0≤x≤xn0:x>xn
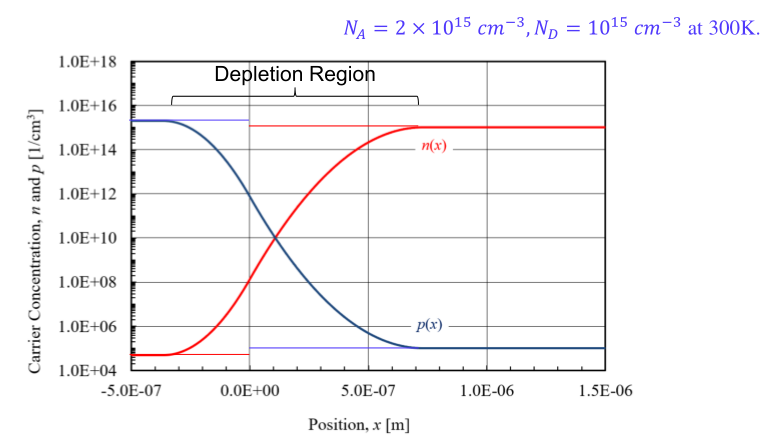
- depletion region에서는 Intrinsic point로 향할수록 majority carrier는 감소하고, minority carrier는 증가
- 즉 depletion region의 바깥 영역에서는 n, p가 같다는 가정이 성립하지 않음
- 하지만 계산의 편의를 위해 단순화하여 ρ(x)=−qNA,qND로 계산
- Diffusion Junction의 경우

- ND−NA의 변화가 곡선으로 나타남
- 계산의 편의를 위해 ρ(x)=q[ND(x)−NA(x)]로 가정 : step junction보다 부정확










